已知公比大于![]() 的等比数列
的等比数列![]() 满足
满足![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)记![]() 为
为![]() 在区间
在区间![]() 中的项的个数,求数列
中的项的个数,求数列![]() 的前
的前![]() 项和
项和![]() .
.
答案
(1)![]() ;(2)
;(2)![]() .
.
【解析】
【分析】
(1)利用基本元的思想,将已知条件转化为![]() 的形式,求解出
的形式,求解出![]() ,由此求得数列
,由此求得数列![]() 的通项公式.
的通项公式.
(2)通过分析数列![]() 的规律,由此求得数列
的规律,由此求得数列![]() 的前
的前![]() 项和
项和![]() .
.
【详解】(1)由于数列![]() 是公比大于
是公比大于![]() 的等比数列,设首项为
的等比数列,设首项为![]() ,公比为
,公比为![]() ,依题意有
,依题意有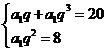 ,解得
,解得![]() ,所以
,所以![]() ,所以数列
,所以数列![]() 的通项公式为
的通项公式为![]() .
.
(2)由于![]() ,所以
,所以
![]() 对应的区间为:
对应的区间为:![]() ,则
,则![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() .
.
所以![]() .
.
【点睛】本小题主要考查等比数列基本量的计算,考查分析思考与解决问的能力,属于中档题.
