已知椭圆C：的离心率为，且过点A（2，1）．

（1）求C的方程：

（2）点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得|DQ|为定值．

答案

（1）；（2）详见解析.

【解析】

【分析】

(1)设出椭圆方程，由题意得到关于a,b,c的方程组，求解方程组即可确定椭圆方程.

(2)设出点M，N的坐标，联立直线方程与椭圆方程可证得直线MN恒过定点，然后结合直角三角形的性质即可确定满足题意的点Q的位置.

【详解】(1)设椭圆方程为：，由题意可得：，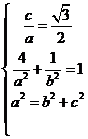

解得：，故椭圆方程为：.

(2)设点.因为AM⊥AN，所以.

整理可得：         ①

设MN的方程为y=kx+m，

联立直线与椭圆方程可得：，

韦达定理可得：

，

，，

代入①式有：，

化简可得：，

即，

据此可得：或，

所以直线MN的方程为或，

即或，

所以直线过定点或.

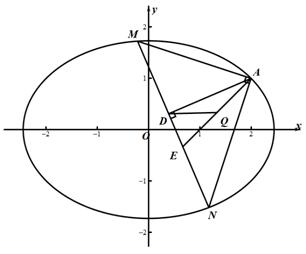
又因为和A点重合，所以舍去，则直线过定点.

由于AE为定值，且△AED为直角三角形，AE为斜边，

所以AE中点Q满足为定值（AE长度的一半）.

由于，故由中点坐标公式可得.

【点睛】解决直线与椭圆的综合问题时，要注意：

(1)注意观察应用题设中每一个条件，明确确定直线、椭圆的条件；

(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．