已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,右焦点为
,右焦点为![]() ,且
,且![]() ,其中
,其中![]() 为原点.
为原点.
(Ⅰ)求椭圆![]() 方程;
方程;
(Ⅱ)已知点![]() 满足
满足![]() ,点
,点![]() 在椭圆上(
在椭圆上(![]() 异于椭圆的顶点),直线
异于椭圆的顶点),直线![]() 与以
与以![]() 为圆心的圆相切于点
为圆心的圆相切于点![]() ,且
,且![]() 为线段
为线段![]() 的中点.求直线
的中点.求直线![]() 的方程.
的方程.
答案
(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,或
,或![]() .
.
【解析】
【分析】
(Ⅰ)根据题意,并借助![]() ,即可求出椭圆的方程;
,即可求出椭圆的方程;
(Ⅱ)利用直线与圆相切,得到![]() ,设出直线
,设出直线![]() 的方程,并与椭圆方程联立,求出
的方程,并与椭圆方程联立,求出![]() 点坐标,进而求出
点坐标,进而求出![]() 点坐标,再根据
点坐标,再根据![]() ,求出直线
,求出直线![]() 的斜率,从而得解.
的斜率,从而得解.
【详解】(Ⅰ)![]() 椭圆
椭圆![]() 的一个顶点为
的一个顶点为![]() ,
,
![]()
![]() ,
,
由![]() ,得
,得![]() ,
,
又由![]() ,得
,得![]() ,
,
所以,椭圆的方程为![]() ;
;
(Ⅱ)![]() 直线
直线![]() 与以
与以![]() 为圆心的圆相切于点
为圆心的圆相切于点![]() ,所以
,所以![]() ,
,
根据题意可知,直线![]() 和直线
和直线![]() 的斜率均存在,
的斜率均存在,
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
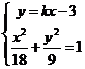 ,消去
,消去![]() ,可得
,可得![]() ,解得
,解得![]() 或
或![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,
,
所以,点![]() 的坐标为
的坐标为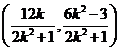 ,
,
因为![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 的坐标为
的坐标为![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,
,
由![]() ,得点
,得点![]() 的坐标为
的坐标为![]() ,
,
所以,直线![]() 的斜率为
的斜率为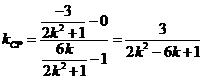 ,
,
又因为![]() ,所以
,所以![]() ,
,
整理得![]() ,解得
,解得![]() 或
或![]() .
.
所以,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
【点睛】本题考查了椭圆标准方程的求解、直线与椭圆的位置关系、直线与圆的位置关系、中点坐标公式以及直线垂直关系的应用,考查学生的运算求解能力,属于中档题.当看到题目中出现直线与圆锥曲线位置关系的问题时,要想到联立直线与圆锥曲线的方程.
