已知函数![]() ,
,![]() 为
为![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,
时,
(i)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(ii)求函数![]() 的单调区间和极值;
的单调区间和极值;
(Ⅱ)当![]() 时,求证:对任意的
时,求证:对任意的![]() ,且
,且![]() ,有
,有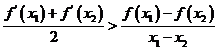 .
.
(Ⅰ)(i)![]() ;(ii)
;(ii)![]() 的极小值为
的极小值为![]() ,无极大值;(Ⅱ)证明见解析.
,无极大值;(Ⅱ)证明见解析.
【解析】
【分析】
(Ⅰ) (i)首先求得导函数的解析式,然后结合导数的几何意义求解切线方程即可;
(ii)首先求得![]() 的解析式,然后利用导函数与原函数的关系讨论函数的单调性和函数的极值即可;
的解析式,然后利用导函数与原函数的关系讨论函数的单调性和函数的极值即可;
(Ⅱ)首先确定导函数的解析式,然后令![]() ,将原问题转化为与
,将原问题转化为与![]() 有关的函数,然后构造新函数,利用新函数的性质即可证得题中的结论.
有关的函数,然后构造新函数,利用新函数的性质即可证得题中的结论.
【详解】(Ⅰ) (i) 当k=6时,![]() ,
,![]() .可得
.可得![]() ,
,![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(ii) 依题意,![]() .
.
从而可得![]() ,
,
整理可得:![]() ,
,
令![]() ,解得
,解得![]() .
.
当x变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
所以,函数g(x)的单调递减区间为(0,1),单调递增区间为(1,+∞);
g(x)的极小值为g(1)=1,无极大值.
(Ⅱ)证明:由![]() ,得
,得![]() .
.
对任意的![]() ,且
,且![]() ,令
,令![]() ,则
,则
![]()
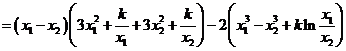

![]() . ①
. ①
令![]() .
.
当x>1时,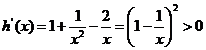 ,
,
由此可得![]() 在
在![]() 单调递增,所以当t>1时,
单调递增,所以当t>1时,![]() ,即
,即![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]()
![]() . ②
. ②
由(Ⅰ)(ii)可知,当![]() 时,
时,![]() ,即
,即![]() ,
,
故![]() ③
③
由①②③可得![]() .
.
所以,当![]() 时,任意的
时,任意的![]() ,且
,且![]() ,有
,有
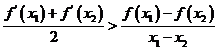 .
.
【点睛】导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,对导数的应用的考查主要从以下几个角度进行:
(1)考查导数的几何意义,往往与解析几何、微积分相联系.
(2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数.
(3)利用导数求函数的最值(极值),解决生活中的优化问题.
(4)考查数形结合思想的应用.
已知![]() 为等差数列,
为等差数列,![]() 为等比数列,
为等比数列,![]() .
.
(Ⅰ)求![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() ;
;
(Ⅲ)对任意的正整数![]() ,设
,设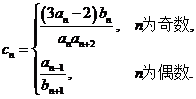 求数列
求数列![]() 的前
的前![]() 项和.
项和.
(Ⅰ)![]() ,
,![]() ;(Ⅱ)证明见解析;(Ⅲ)
;(Ⅱ)证明见解析;(Ⅲ)![]() .
.
【解析】
【分析】
(Ⅰ)由题意分别求得数列的公差、公比,然后利用等差、等比数列的通项公式得到结果;
(Ⅱ)利用(Ⅰ)的结论首先求得数列![]() 前n项和,然后利用作差法证明即可;
前n项和,然后利用作差法证明即可;
(Ⅲ)分类讨论n为奇数和偶数时数列的通项公式,然后分别利用指数型裂项求和和错位相减求和计算![]() 和
和![]() 的值,据此进一步计算数列
的值,据此进一步计算数列![]() 的前2n项和即可.
的前2n项和即可.
【详解】(Ⅰ)设等差数列![]() 的公差为
的公差为![]() ,等比数列
,等比数列![]() 的公比为q.
的公比为q.
由![]() ,
,![]() ,可得d=1.
,可得d=1.
从而![]() 的通项公式为
的通项公式为![]() .
.
由![]() ,
,
又q≠0,可得![]() ,解得q=2,
,解得q=2,
从而![]() 的通项公式为
的通项公式为![]() .
.
(Ⅱ)证明:由(Ⅰ)可得![]() ,
,
故![]() ,
,![]() ,
,
从而![]() ,
,
所以![]() .
.
(Ⅲ)当n![]() 奇数时,
奇数时,![]() ,
,
当n为偶数时,![]() ,
,
对任意的正整数n,有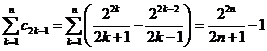 ,
,
和![]() ①
①
由①得![]() ②
②
由①②得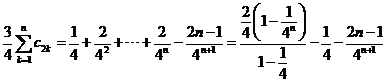 ,
,
由于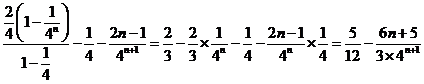 ,
,
从而得:![]() .
.
因此,![]() .
.
所以,数列![]() 的前2n项和为
的前2n项和为![]() .
.
【点睛】本题主要考查数列通项公式的求解,分组求和法,指数型裂项求和,错位相减求和等,属于中等题.
已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,右焦点为
,右焦点为![]() ,且
,且![]() ,其中
,其中![]() 为原点.
为原点.
(Ⅰ)求椭圆![]() 方程;
方程;
(Ⅱ)已知点![]() 满足
满足![]() ,点
,点![]() 在椭圆上(
在椭圆上(![]() 异于椭圆的顶点),直线
异于椭圆的顶点),直线![]() 与以
与以![]() 为圆心的圆相切于点
为圆心的圆相切于点![]() ,且
,且![]() 为线段
为线段![]() 的中点.求直线
的中点.求直线![]() 的方程.
的方程.
(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,或
,或![]() .
.
【解析】
【分析】
(Ⅰ)根据题意,并借助![]() ,即可求出椭圆的方程;
,即可求出椭圆的方程;
(Ⅱ)利用直线与圆相切,得到![]() ,设出直线
,设出直线![]() 的方程,并与椭圆方程联立,求出
的方程,并与椭圆方程联立,求出![]() 点坐标,进而求出
点坐标,进而求出![]() 点坐标,再根据
点坐标,再根据![]() ,求出直线
,求出直线![]() 的斜率,从而得解.
的斜率,从而得解.
【详解】(Ⅰ)![]() 椭圆
椭圆![]() 的一个顶点为
的一个顶点为![]() ,
,
![]()
![]() ,
,
由![]() ,得
,得![]() ,
,
又由![]() ,得
,得![]() ,
,
所以,椭圆的方程为![]() ;
;
(Ⅱ)![]() 直线
直线![]() 与以
与以![]() 为圆心的圆相切于点
为圆心的圆相切于点![]() ,所以
,所以![]() ,
,
根据题意可知,直线![]() 和直线
和直线![]() 的斜率均存在,
的斜率均存在,
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
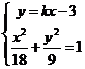 ,消去
,消去![]() ,可得
,可得![]() ,解得
,解得![]() 或
或![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,
,
所以,点![]() 的坐标为
的坐标为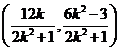 ,
,
因为![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 的坐标为
的坐标为![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,
,
由![]() ,得点
,得点![]() 的坐标为
的坐标为![]() ,
,
所以,直线![]() 的斜率为
的斜率为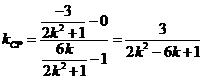 ,
,
又因为![]() ,所以
,所以![]() ,
,
整理得![]() ,解得
,解得![]() 或
或![]() .
.
所以,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
【点睛】本题考查了椭圆标准方程的求解、直线与椭圆的位置关系、直线与圆的位置关系、中点坐标公式以及直线垂直关系的应用,考查学生的运算求解能力,属于中档题.当看到题目中出现直线与圆锥曲线位置关系的问题时,要想到联立直线与圆锥曲线的方程.
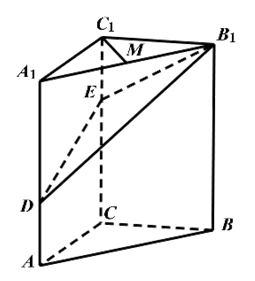
如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 分别在棱
分别在棱![]() 和棱
和棱![]() 上,且
上,且![]() 为棱
为棱![]() 的中点.
的中点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(Ⅰ)证明见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
【分析】
以![]() 为原点,分别以
为原点,分别以![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系.
轴的正方向建立空间直角坐标系.
(Ⅰ)计算出向量![]() 和
和![]() 的坐标,得出
的坐标,得出![]() ,即可证明出
,即可证明出![]() ;
;
(Ⅱ)可知平面![]() 的一个法向量为
的一个法向量为![]() ,计算出平面
,计算出平面![]() 的一个法向量为
的一个法向量为![]() ,利用空间向量法计算出二面角
,利用空间向量法计算出二面角![]() 的余弦值,利用同角三角函数的基本关系可求解结果;
的余弦值,利用同角三角函数的基本关系可求解结果;
(Ⅲ)利用空间向量法可求得直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【详解】依题意,以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立空间直角坐标系(如图),
轴的正方向建立空间直角坐标系(如图),

可得![]() 、
、![]() 、
、![]() 、
、![]() 、
、
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
(Ⅰ)依题意,![]() ,
,![]() ,
,
从而![]() ,所以
,所以![]() ;
;
(Ⅱ)依题意,![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
![]() ,
,![]() .
.
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则 ,即
,即![]() ,
,
不妨设![]() ,可得
,可得![]() .
.
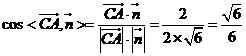 ,
,
![]() .
.
所以,二面角![]() 的正弦值为
的正弦值为![]() ;
;
(Ⅲ)依题意,![]() .
.
由(Ⅱ)知![]() 为平面
为平面![]() 的一个法向量,于是
的一个法向量,于是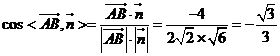 .
.
所以,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【点睛】本题考查利用空间向量法证明线线垂直,求二面角和线面角的正弦值,考查推理能力与计算能力,属于中档题.
在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() .已知
.已知![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)求![]() 的值;
的值;
(Ⅲ)求![]() 的值.
的值.
(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
【分析】
(Ⅰ)直接利用余弦定理运算即可;
(Ⅱ)由(Ⅰ)及正弦定理即可得到答案;
(Ⅲ)先计算出![]() 进一步求出
进一步求出![]() ,再利用两角和的正弦公式计算即可.
,再利用两角和的正弦公式计算即可.
【详解】(Ⅰ)在![]() 中,由
中,由![]() 及余弦定理得
及余弦定理得
![]() ,
,
又因为![]() ,所以
,所以![]() ;
;
(Ⅱ)在![]() 中,由
中,由![]() ,
,![]() 及正弦定理,可得
及正弦定理,可得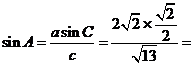
![]() ;
;
(Ⅲ)由![]() 知角
知角![]() 为锐角,由
为锐角,由![]() ,可得
,可得![]()
![]() ,
,
进而![]() ,
,
所以![]()
![]() .
.
【点晴】本题主要考查正、余弦定理解三角形,以及三角恒等变换在解三角形中的应用,考查学生的数学运算能力,是一道容易题.
本卷还有15题,登录并加入会员即可免费使用哦~

该作品由: 用户大河分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。