某地为响应关于生态文明建设的指示精神,大力开展“青山绿水”工程,造福于民.为此,当地政府决定将一扇形(如图)荒地改造成市民休闲中心,其中扇形内接矩形区域为市民健身活动场所,其余区域(阴影部分)改造为景观绿地(种植各种花草).已知该扇形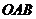 的半径为200米,圆心角
的半径为200米,圆心角 ,点
,点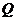 在
在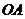 上,点
上,点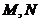 在
在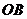 上,点
上,点 在弧
在弧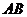 上,设
上,设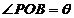 .
.
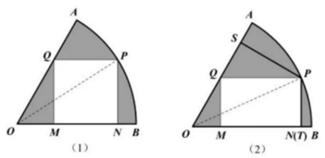
(1)若矩形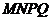 是正方形,求
是正方形,求 的值;
的值;
(2)为方便市民观赏绿地景观,从 点处向
点处向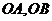 修建两条观赏通道
修建两条观赏通道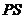 和
和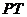 (宽度不计),使
(宽度不计),使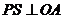 ,
,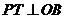 ,其中
,其中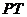 依
依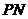 而建,为让市民有更多时间观赏,希望
而建,为让市民有更多时间观赏,希望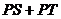 最长,试问:此时点
最长,试问:此时点 应在何处?说明你的理由.
应在何处?说明你的理由.
答案
(1)矩形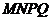 是正方形时,
是正方形时,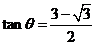 (2)当
(2)当 是
是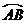 的中点时,
的中点时,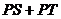 最大
最大
【解析】
试题分析:(1)因为四边形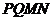 是扇形的内接正方形,所以
是扇形的内接正方形,所以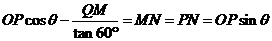 ,注意到
,注意到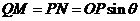 ,代入前者就可以求出
,代入前者就可以求出 . (2)由题设可由
. (2)由题设可由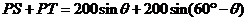 ,
,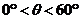 ,利用两角差的正弦和辅助角公式把
,利用两角差的正弦和辅助角公式把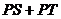 化成
化成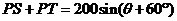 的形式,从而求出
的形式,从而求出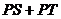 的最大值.
的最大值.
 解析:(1)在
解析:(1)在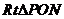 中,
中, 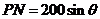 ,
,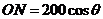 ,在
,在 中,
中, 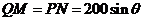 ,
,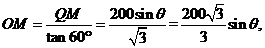 所以
所以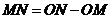
 ,因为矩形
,因为矩形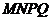 是正方形,
是正方形, ,所以
,所以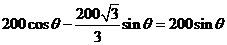 ,所以
,所以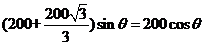 ,所以
,所以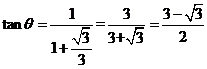 .
.
(2)因为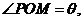 所以
所以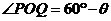 ,
,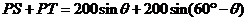

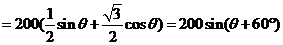 ,
,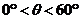 .所以
.所以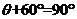 , 即
, 即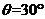 时,
时,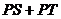 最大,此时
最大,此时 是
是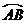 的中点.
的中点.
答:(1)矩形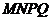
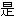 正方形时,
正方形时,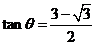 ;
;
(2)当 是
是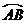 的中点时,
的中点时,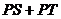 最大.
最大.


 中,已知
中,已知 ,问题就无解。如果有解,是一解,还是两解。解得个数讨论见下表:
,问题就无解。如果有解,是一解,还是两解。解得个数讨论见下表:


