如图,在直角坐标系![]() 中,过坐标原点
中,过坐标原点![]() 作曲线
作曲线![]() 的切线,切点为
的切线,切点为![]() ,过点
,过点![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,向矩形
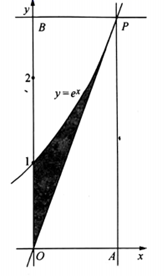
,向矩形![]() 中随机撒一粒黄豆,则它落到阴影部分的概率为( )
中随机撒一粒黄豆,则它落到阴影部分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
答案
A
【分析】
先设出切点![]() ,利用切线过原点求出切点P的坐标,再用积分求出阴影部分的面积,最后用几何概型求得结果.
,利用切线过原点求出切点P的坐标,再用积分求出阴影部分的面积,最后用几何概型求得结果.
【详解】
设切点![]() ,
,![]()
所以切线方程![]() ,又因为过原点
,又因为过原点
所以![]() 解得
解得![]()
所以点P![]()
因为![]() 与
与![]() 轴在
轴在![]() 围成的面积是
围成的面积是![]()
则阴影部分的面积为![]()
而矩形![]() 的面积为
的面积为![]()
故向矩形![]() 中随机撒一粒黄豆,则它落到阴影部分的概率为
中随机撒一粒黄豆,则它落到阴影部分的概率为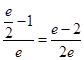
故选A
【点睛】
本题主要考查了几何概型,但是解题的关键是在于对于切点和积分的运用是否熟练,属于中档题.

 总是接近于某个常数,在它附近摆动。这时就把这个常数叫做事件A的概率,记作P(A)。
总是接近于某个常数,在它附近摆动。这时就把这个常数叫做事件A的概率,记作P(A)。  总是接近于区间[0,1]中的某个常数,我们就把这个常数叫做事件A的概率,记作P(A)。
总是接近于区间[0,1]中的某个常数,我们就把这个常数叫做事件A的概率,记作P(A)。