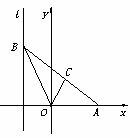如图所示椭圆
的左、右顶点分别为
，
，上、下顶点分别为
，
，右焦点为
，
，离心率
.
（1）求椭圆
的方程；
（2）过点
作斜率为
的直线
与椭圆交于点
，
（点在第一象限），直线
与直线
交于点
，求点的坐标.
答案
（1）
；（2）
.
【分析】
（1）根据
及
可求
的值，从而可得椭圆的方程.
（2）联立直线方程和椭圆方程可求
的坐标，再求得直线
的方程后可得点
的坐标.
【详解】
解：（1）由及，
可知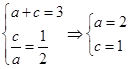
，
所以
，
所以椭圆
的方程为.
（2）依题可设过点
且斜率为
的直线
，
，
，
联立方程组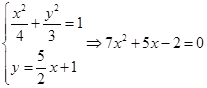
，
解得
，
，则
，
，
所以
，
，
由（1）知，
，
.
所以直线
，①
直线
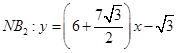，②
由①②，解得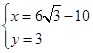
，
所以点的坐标为.
【点睛】
本题考查椭圆方程的求法、直线与椭圆的相交时交点坐标的求法、直线与直线的交点的求法，后两者均需联立曲线的方程，消元后求解即可，本题属于中档题.
