已知双曲线
的两条渐近线分别与抛物线
交于第一、四象限的A，B两点，设抛物线焦点为F，若
，则双曲线的离心率为（ ）
A．
B．
C．
D．
答案
B
【分析】
求得双曲线的渐近线方程，联立抛物线方程，求得A，B的坐标，以及F的坐标，设AF的倾斜角为
，由二倍角的余弦公式和同角的基本关系式，以及直线的斜率公式，双曲线的离心率公式，计算可得所求值.
【详解】
解：双曲线的两条渐近线方程为
，
由抛物线和
，联立可得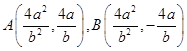
，
由抛物线的方程可得
，
设AF的倾斜角为，斜率为
，
而
，
解得
（负的舍去），
设
，可得
，解得
，
则
，
故选：B.
【点睛】
本题考查双曲线的方程和性质，考查三角函数的恒等变换，以及化简运算能力，属于中档题.
(B)
