高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型，在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块，小木块之间留有适当的空隙作为通道，前面挡有一块玻璃，让一个小球从高尔顿板上方的通道口落下，小球在下落的过程中与层层小木块碰撞，且等可能向左或向右滚下，最后掉入高尔顿板下方的某一球槽内 . 如图 1 所示的高尔顿板有 7 层小木块，小球从通道口落下，第一次与第 2 层中间的小木块碰撞，以 的概率向左或向右滚下，依次经过 6 次与小木块碰撞，最后掉入编号为 1 ， 2 ， … ， 7 的球槽内 . 例如小球要掉入 3 号球槽，则在 6 次碰撞中有 2 次向右 4 次向左滚下 .

（ 1 ）如图 1 ，进行一次高尔顿板试验，求小球落入 5 号球槽的概率；

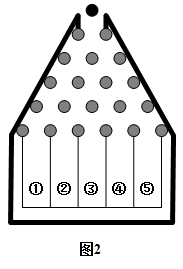
（ 2 ）小红､小明同学在研究了高尔顿板后，利用高尔顿板来到社团文化节上进行盈利性 “ 抽奖 ” 活动 . 小红使用图 1 所示的高尔顿板，付费 6 元可以玩一次游戏，小球掉入 m 号球槽得到的奖金为 元，其中 . 小明改进了高尔顿板 ( 如图 2) ，首先将小木块减少成 5 层，然后使小球在下落的过程中与小木块碰撞时，有 的概率向左， 的概率向右滚下，最后掉入编号为 1 ， 2 ， …… ， 5 的球槽内，改进高尔顿板后只需付费 4 元就可以玩一次游戏，小球掉入 n 号球槽得到的奖金为 元，其中 . 两位同学的高尔顿板游戏火爆进行，很多同学参加了游戏，你觉得小红和小明同学谁的盈利多？请说明理由 .

答案

（ 1 ） ；（ 2 ）小明的盈利多，理由见解析 .

【分析】

（ 1 ）设这个小球掉入 5 号球槽为事件 ，掉入 5 号球槽，需要向右 4 次向左 2 次，利用独立重复试验的概率计算可得；

（ 2 ） 的可能取值为 0 ， 4 ， 8 ， 12 ，分别求出对应的概率，列出分布列求出 ； 的可能取值为 0 ， 1 ， 4 ， 9 ，求出对应的概率，列出分布列求出 ，比较 与 的大小，确定小明的盈利多 .

【详解】

（ 1 ）设这个小球掉入 5 号球槽为事件 ，掉入 5 号球槽，需要向右 4 次向左 2 次，所以 ，

所以这个小球掉入 5 号球槽的概率为 .

（ 2 ）小红的收益计算如下：每一次游戏中， 的可能取值为 0 ， 4 ， 8 ， 12.

，

，

，

.

一次游戏付出的奖金 ，则小红的收益为 .

小明的收益计算如下：每一次游戏中， 的可能取值为 0 ， 1 ， 4 ， 9.

，

，

，

.

一次游戏付出的奖金 ，则小明的收益为 .

显然， ，所以小明的盈利多 .

【点睛】

方法点睛：本题考查独立重复试验的概率问题以及离散型随机变量的分布列和数学期望，求离散型随机变量的分布列，首先要根据具体情况确定 的取值情况，然后利用排列，组合，概率知识求出 取各个值时对应的概率，对应服从某种特殊分布的随机变量，其分布列可以直接应用公式给出，考查学生逻辑推理能力与计算能力，属于中档题 .