如图，在四棱锥 中， 底面 ，底面 为平行四边形， ，且 ， ， 是棱 的中点 .

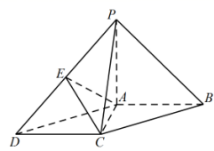
（ 1 ）求证： 平面 ；

（ 2 ）求直线 与平面 所成角的正弦值；

（ 3 ）在线段 上 ( 不含端点 ) 是否存在一点 ，使得二面角 的余弦值为 ？若存在，确定 的位置；若不存在，请说明理由 .

答案

（ 1 ）证明见解析 . （ 2 ） . （ 3 ）存在，

【分析】

（ 1 ）连接 交 于点 ，连接 ，可证 ，从而得线面平行；

（ 2 ）由题意以 为坐标原点，分别以 所在直线为 轴， 轴， 轴建立空间直角坐标系，可用向量法求出线面角；

（ 3 ）在（ 2 ）基础上，设 ，求出平面 和平面 （（ 2 ）中已有）法向量，由法向量夹角与二面角的关系可求得 ．

【详解】

（ 1 ）连接 交 于点 ，连接 .

∵ 是平行四边形， ∴ 是 的中点 . 又 是 的中点， ∴

又 平面 ， 平面 ， ∴ 平面 ；

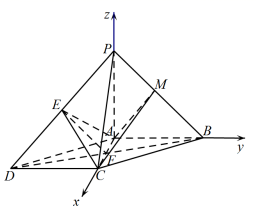
（ 2 ）以 为坐标原点，分别以 所在直线为 轴， 轴， 轴建立如图所示的空间直角坐标系，则 ， ， ， ， ， .

设平面 的法向量为 .

∵ ，

∴ 即

不妨取 ，得

又 .

设直线 与平面 所成的角为 ，

则 ，

即直线 与平面 所成角的正弦值为 ．

（ 3 ）假设在线段 上 ( 不含端点 ) 存在一点 ，使得二面角 的余弦值为 . 连接 . 设 ， 得 .

设平面 的法向量为 .

∵ ，

∴ 即

不妨取 ，得

设二面角 的平面角为 ，

则 .

化简得 ，

解得 ，或 .

∵ 二面角 的余弦值为 ，

∴ .

∴ 在线段 上存在一点 ，且 ，使得二面角 的余弦值为 .

【点睛】

本题考查证明线面平行，考查用空间向量法求线面角和二面角，用线面平行的判定定理证线面平行是证明线面平行的掌握方法．在图形中有两两相互垂直的三条直线时，常常是建立空间直角坐标系，用空间向量法研究空间角．这种方法化证明为计算，减少学生的逻辑思维量，但增加了计算量．