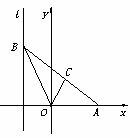已知椭圆 ， ， 分别为椭圆的左右焦点， 为椭圆上任意一点

（ 1 ）若 ，求 的面积；

（ 2 ）是否存在着直线 ，使得当 经过椭圆左顶点 且与椭圆相交于点 ，点 与点 关于 轴对称，满足 ，若存在，请求出直线 的方程；若不存在，请说明理由．

答案

（ 1 ） ；（ 2 ） 或 ，理由见解析 .

【分析】

（ 1 ）联立方程解得 ， ， ，判断为直角三角形，再利用面积公式计算得到答案 .

（ 2 ）联立方程计算 ，根据 计算得到答案 .

【详解】

（ 1 ） ， ，

（ 2 ）设 故

且 ，

故

即 故

或

【点睛】

本题考查了面积和椭圆与直线的位置关系，意在考查学生的综合应用能力和计算能力 .