赵爽是我国古代数学家、天文学家．约公元 222 年，赵爽为《周髀算经》一书作序时，介绍了 “ 勾股圆方程 ” ，亦称 “ 赵爽弦图 ” ，它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形．如图是一张弦图，已知大正方形的面积为 25 ，小正方形的面积为 1 ，若直角三角形较小的锐角为 ，则 的值为（ ）

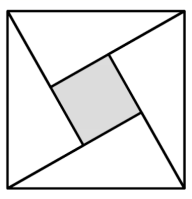
A ． 7 B ． C ． 4 D ． 9

答案

A

【分析】

根据题意求出一个直角三角形的直角边，即可求出锐角 的正切值，从而利用两角和的正切公式即可求出结果．

【详解】

解：根据图形的特点，设四个全等的直角三角形的一条直角边为 ，另一条为 ，

所以 ，

解得 ，

所以 ，

所以 ，

故 ．

故选： A ．