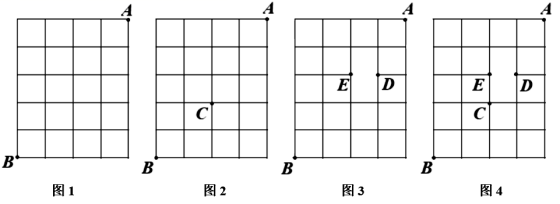
（ 1 ）如图 1 所示，某地有南北街道 5 条，东西街道 6 条，一邮电员从该地东北角的邮局 出发，送信到西南角的 地，要求所走的路程最短，共有多少种不同的走法？

（ 2 ）如图 2 所示，某地有南北街道 5 条，东西街道 6 条，一邮电员从该地东北角的邮局 出发，送信到西南角的 地，已知 地（十字路口）在修路，无法通行，要求所走的路程最短，共有多少种不同的走法？

（ 3 ）如图 3 所示，某地有南北街道 5 条，东西街道 6 条（注意有一段 不通），一邮电员从该地东北角的邮 局出发，送信到西南角的 地，要求所走的路程最短，共有多少种不同的走法？

（ 4 ）如图 4 所示，某地有南北街道 5 条，东西街道 6 条，已知 地（十字路口）在修路，无法通行，且有一段路程 无法通行，一邮递员该地东北角的邮局 出发，送信到西南角的 地，要求所走的路程最短，有多少种不同的走法？

答案

（ 1 ） 126 ；（ 2 ） 66 ；（ 3 ） ；（ 4 ） 54 ．

【分析】

（ 1 ）由 A 到 B 所走路程最短需要向下走 5 次，向左走 4 次，转化为组合问题， 9 次运动中哪 4 次向左即可求解；

（ 2 ）先分析由 A 经 C 到 B 的走法，再由间接法即可求出不经过 C 的走法；

（ 3 ）先分析经过 ED 的走法，再由间接法求解；

（ 4 ）先计算经过 DE 且经过 C 的走法，再结合（ 1 ）（ 2 ）（ 3 ）利用间接法求解 .

【详解】

（ 1 ）由题意，由 A 到 B 的最短距离需要 9 步完成，其中向下走 5 步，向左走 4 步，

由组合知识可知，不同的走法共有 种 .

(2) 若先经过 C 再到 B ，需向下走 3 步，向左走 2 步，有 种走法，由 C 到 B 需向下运动 2 步，向左运动 2 步，有 种走法，故先经过 C 再到 B 共有 ，

所以不经过 C 共有 种走法 .

(3) 经过 ED, 需要 3 步由 A 到 D ，再需要 5 步由 E 到 B ，由 A 到 D 共有 种走法，由 E 到 B 共有 种走法，所以经过 ED 的走法共有 种，

故不经过 ED 的走法共有 种 .

(4) 由 A 经过 DE 到 C 的走法共有 ，再由 C 到 B 需要向下、向左各 2 步共有 种走法，

故经过 DE 到 C 再到 B 的走法共有 种走法，

所以不经过 DE 也不经过 C 的走法共有 种 .