若 是以
为直角顶点的三角形，且面积为
，设向量
，
，
，则关于
下列说法正确的是（ ）
A ．有最大值为 B ．有最小值为
C ．有最大值为 D ．有最小值为
答案
A
【解析】
【分析】
根据题意设出点坐标，结合向量数量积的坐标运算公式和基本不等式求解即可 .
【详解】
因为 是以
为直角顶点的三角形，
所以如下图所示，不妨设 ，
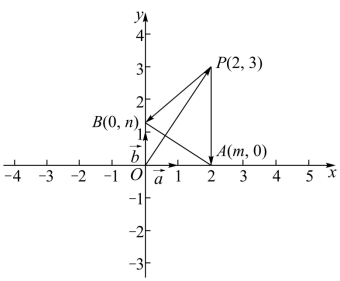
因为 面积为
，
所以 ，即
，
因为向量 ，
，
，
所以 ，即
，
所以 ，
所以 ，
当且仅当 ，即
时等号成立，
所以 有最大值为
.
故选： A
，
，作
称为向量
，
的夹角，当
＝0时，
，
同向，当
＝π时，
，
反向，
时，
垂直。
，
，它们的夹角为
，我们把数量
叫做
与
的数量积（或内积或点积），记作：
，即
。
叫
在
上的投影。
等于
的模
与
在
上的投影
的乘积。
；
；
；
；
，
同向时，
；当
与
反向时，
；当
为锐角时，
为正且
，
不同向，
；当
为钝角时，
为负且
，
不反向，
。 
