在唐诗 “ 白日登山望烽火，黄昏饮马傍交河 ” 中隐含着一个有趣的数学问题 ——“ 将军饮马 ” 问题，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，设军营所在区域为 ，若将军从点 处出发，河岸线所在直线方程为 ，并假定将军只要到达军营所在区域即认为回到军营，则当 “ 将军饮马 ” 的总路程最短时，将军去往河边饮马的行走路线所在的直线方程为（ ）

A ． B ．

C ． D ．

答案

B

【分析】求圆心 C 关于直线 的对称点 B 的坐标，结合图形分析可得 .

【详解】军营所在区域为 ，即军营在以 为圆心， 1 为半径的圆内和圆上 .

设圆心 C 关于直线 的对称点的坐标为 B ，

则 ，解得 .

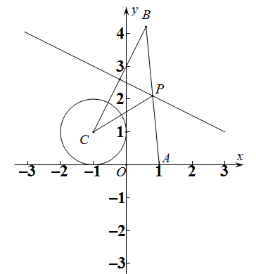
如图，由对称性可知，

所以，当将军去往河边饮马的行走路线所在的直线经过 ， 两点时， “ 将军饮马 ” 的总路程最短，

因为 ，所以该直线方程为 ，即 .

故选： B