在直角坐标系中,曲线 的参数方程为
,(
为参数,
),以
轴的正半轴为极轴建立极坐标系,曲线
在极坐标系中的方程为
.若曲线
与
有两个不同的交点,则实数
的取值范围是( )
A . B .
C .
D .
答案
A
【分析】消去参数化参数方程为普通方程,由公式 可化极坐标方程为直角坐标方程,由直角坐标方程作出图形,利用数形结合可得参数范围.
【详解】由 ,曲线
的普通方程是
(
),
由 得曲线
的直角坐标方程是
,即
,
作出曲线 ,它是单位圆的上半圆,如图,
直线 过点
时,
,
直线 与半圆相切时,
,
(
舍去),
由图可得 时,直线
与曲线
前两个公共点.
故选: A .
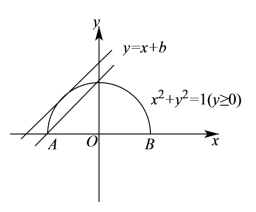

 ,半径为
,半径为 的圆;
的圆;  ;
;  ,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为
,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为 。
。 
 >0时,表示圆心在
>0时,表示圆心在 =0时,表示点
=0时,表示点 <0时,不表示任何图形。
<0时,不表示任何图形。  的系数相同且不等于零;
的系数相同且不等于零; 的方程表示圆的条件:
的方程表示圆的条件: 即
即

















