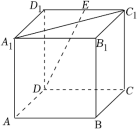
如图所示，在正方体 中，若 是 的中点，则异面直线 与 所成角的大小为 _______ ．（结果用反三角函数表示）

答案

【分析】取 的中点 F ，连接 DF ，得到 是异面直线 与 所成的角，然后利用余弦定理求解 .

【详解】解：如图所示：

取 的中点 F ，连接 DF ，

则 是异面直线 与 所成的角，

设正方体的棱长为 ，

则 ，

所以 ，

，

所以 ，

故答案为：