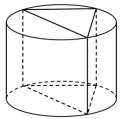
如图，某加工厂要在一圆柱体材料中打磨出一个直三棱柱模具，已知该圆柱底面圆面积为 ，高为 6 ，则能截得直三棱柱体积最大为（ ）

A ． B ． C ． D ．

答案

B

【分析】根据直三棱柱的定义及三角形的面积公式，再利用正弦定理及三元基本不等式，结合棱柱的体积公式即可求解 .

【详解】由题意可知，设底面圆的半径为 ，则 , 解得 .

因为直三棱柱的定义可知，要使能截得直三棱柱体积最大，只需要圆的内接三角形面积最大即可，

.

当且仅当 ，即 时。等号成立，

所以三角形是正三角形时，圆的内接三角形面积最大，

.

所以能截得直三棱柱体积最大为 .

故选： B.