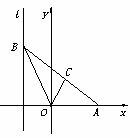已知双曲线 的左焦点为 F ，过 F 且斜率为 的直线交双曲线于点 ，交双曲线的渐近线于点 且 ．若 ，则双曲线的离心率是 _________ ．

答案

【分析】联立直线 和渐近线 方程，可求出点 ，再根据 可求得点 ，最后根据点 在双曲线上，即可解出离心率．

【详解】过 且斜率为 的直线 ，渐近线 ，

联立 ，得 ，由 ，得

而点 在双曲线上，于是 ，解得： ，所以离心率 .

故答案为： ．