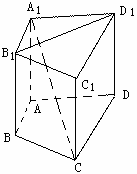
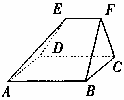
如图，已知 和 都是直角梯形， ， ， ， ， ， ，二面角 的平面角为 ．设 M ， N 分别为 的中点．

(1) 证明： ；

(2) 求直线 与平面 所成角的正弦值．

答案

(1) 证明见解析；

(2) ．

【分析】（ 1 ）过点 、 分别做直线 、 的垂线 、 并分别交于点 、 ，由平面知识易得 ，再根据二面角的定义可知， ，由此可知， ， ，从而可证得 平面 ，即得 ；

（ 2 ）由（ 1 ）可知 平面 ，过点 做 平行线 ，所以可以以点 为原点， ， 、 所在直线分别为 轴、 轴、 轴建立空间直角坐标系 ，求出平面 的一个法向量，以及 ，即可利用线面角的向量公式解出．

【详解】（ 1 ）过点 、 分别做直线 、 的垂线 、 并分别交于点 、 ．

∵ 四边形 和 都是直角梯形， ， ，由平面几何知识易知， ，则四边形 和四边形 是矩形， ∴ 在 Rt 和 Rt ， ，

∵ ，且 ，

∴ 平面 是二面角 的平面角，则 ，

∴ 是正三角形，由 平面 ，得平面 平面 ，

∵ 是 的中点， ，又 平面 ， 平面 ，可得 ，而 ， ∴ 平面 ，而 平面 ．

（ 2 ）因为 平面 ，过点 做 平行线 ，所以以点 为原点， ， 、 所在直线分别为 轴、 轴、 轴建立空间直角坐标系 ，

设 ，则 ，

设平面 的法向量为

由 ，得 ，取 ，

设直线 与平面 所成角为 ，

∴ ．