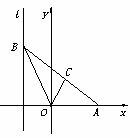如图,已知椭圆 .设 A , B 是椭圆上异于
的两点,且点
在线段
上,直线
分别交直线
于 C , D 两点.

(1) 求点 P 到椭圆上点的距离的最大值;
(2) 求 的最小值.
答案
(1) ;
(2) .
【分析】( 1 )设 是椭圆上任意一点 , 再根据两点间的距离公式求出
,再根据二次函数的性质即可求出;
( 2 )设直线 与椭圆方程联立可得
,再将直线
方程与
的方程分别联立,可解得点
的坐标,再根据两点间的距离公式求出
,最后代入化简可得
,由柯西不等式即可求出最小值.
【详解】( 1 )设 是椭圆上任意一点 ,
,
,当且仅当
时取等号,故
的最大值是
.
( 2 )设直线 , 直线
方程与椭圆
联立 , 可得
, 设
,所以
,
因为直线 与直线
交于
,
则 , 同理可得 ,
. 则
,
当且仅当 时取等号,故
的最小值为
.
【点睛】本题主要考查最值的计算,第一问利用椭圆的参数方程以及二次函数的性质较好解决,第二问思路简单,运算量较大,求最值的过程中还使用到柯西不等式求最值,对学生的综合能力要求较高,属于较难题.