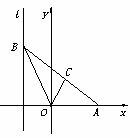设 F 为抛物线 的焦点，点 A 在 C 上，点 ，若 ，则 （ ）

A ． 2 B ． C ． 3 D ．

答案

B

【分析】根据抛物线上的点到焦点和准线的距离相等，从而求得点 的横坐标，进而求得点 坐标，即可得到答案 .

【详解】由题意得， ，则 ，

即点 到准线 的距离为 2 ，所以点 的横坐标为 ，

不妨设点 在 轴上方，代入得， ，

所以 .

故选： B