已知双曲线Γ1:![]() 与圆Γ2:x2+y2=4+b2(b>0)交于点A(xA,yA)(第一象限),曲线Γ为Γ1、Γ2上取满足x>|xA|的部分.
与圆Γ2:x2+y2=4+b2(b>0)交于点A(xA,yA)(第一象限),曲线Γ为Γ1、Γ2上取满足x>|xA|的部分.
(1)若xA=![]() ,求b的值;
,求b的值;
(2)当b=![]() ,Γ2与x轴交点记作点F1、F2,P是曲线Γ上一点,且在第一象限,且|PF1|=8,求∠F1PF2;
,Γ2与x轴交点记作点F1、F2,P是曲线Γ上一点,且在第一象限,且|PF1|=8,求∠F1PF2;
(3)过点D(0,![]() )斜率为-
)斜率为-![]() 的直线l与曲线Γ只有两个交点,记为M、N,用b表示
的直线l与曲线Γ只有两个交点,记为M、N,用b表示![]() ,并求
,并求![]() 的取值范围.
的取值范围.
(1)2 (2)arccos![]() (3)(6+2
(3)(6+2![]() ,+∞)
,+∞)
【解析】解:(1)由xA=![]() ,点A为曲线Γ1与曲线Γ2的交点,联立
,点A为曲线Γ1与曲线Γ2的交点,联立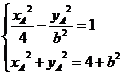 ,解得yA=
,解得yA=![]() ,b=2;
,b=2;
(2)由题意可得F1,F2为曲线Γ1的两个焦点,
由双曲线的定义可得|PF1|-|PF2|=2a,又|PF1|=8,2a=4,
所以|PF2|=8-4=4,因为b=![]() ,则c=
,则c=![]() =3,
=3,
所以|F1F2|=6,
在△PF1F2中,由余弦定理可得cos∠F1PF2=![]() =
=![]()
由0<∠F1PF2<π,可得∠F1PF2=arccos![]() ;
;
(3)设直线l:![]() ,可得原点O到直线l的距离d=
,可得原点O到直线l的距离d=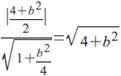 ,所以直线l是圆的切线,设切点为M,
,所以直线l是圆的切线,设切点为M,
所以kOM=![]() ,并设OM:y=
,并设OM:y=![]() x与圆x2+y2=4+b2联立,可得x2+
x与圆x2+y2=4+b2联立,可得x2+![]() =4+b2,
=4+b2,
可得x=b,y=2,即M(b,2),
注意直线l与双曲线的斜率为负的渐近线平行,
所以只有当yA>2时,直线l才能与曲线Γ有两个交点,
由 ,
,
所以有4<![]() ,解得b2>2+2
,解得b2>2+2![]() 或b2<2-2
或b2<2-2![]() (舍去),
(舍去),
因为![]() 为
为![]() 在
在![]() 上的投影可得,
上的投影可得,![]() =4+b2,
=4+b2,
所以![]() =4+b2>6+2
=4+b2>6+2![]() ,
,
则![]() ∈(6+2
∈(6+2![]() ,+∞).
,+∞).
【考点】平面向量数量积的性质及其运算;直线与双曲线的综合.
【专题】方程思想;综合法;圆锥曲线的定义、性质与方程;数学运算.
【分析】(1)联立曲线Γ1与曲线Γ2的方程,以及xA=![]() ,解方程可得b;
,解方程可得b;
(2)由双曲线的定义和三角形的余弦定理,计算可得所求角;
(3)设直线l:![]() ,求得O到直线l的距离,判断直线l与圆的关系:相切,可设切点为M,考虑双曲线的渐近线方程,只有当yA>2时,直线l才能与曲线Γ有两个交点,解不等式可得b的范围,由向量投影的定义求得
,求得O到直线l的距离,判断直线l与圆的关系:相切,可设切点为M,考虑双曲线的渐近线方程,只有当yA>2时,直线l才能与曲线Γ有两个交点,解不等式可得b的范围,由向量投影的定义求得![]() ,进而得到所求范围.
,进而得到所求范围.
【点评】本题考查双曲线与圆的定义和方程、性质,考查直线和圆的方程、双曲线的方程的联立,以及向量的数量积的几何意义,考查方程思想和化简运算能力,属于中档题.
已知函数f(x)=sinωx,ω>0.
(1)f(x)的周期是4π,求ω,并求f(x)=![]() 的解集;
的解集;
(2)已知ω=1,g(x)=f2(x)+![]() f(-x)f(
f(-x)f(![]() -x),
-x),![]() ,求g(x)的值域.
,求g(x)的值域.
(1){x|x=4kπ+![]() 或x=4kπ+
或x=4kπ+![]() ,k∈Z} (2)
,k∈Z} (2)![]()
【解析】解:(1)由于f(x)的周期是4π,所以ω=![]() ,所以f(x)=sin
,所以f(x)=sin
![]() x.
x.
令sin![]() x=
x=![]() ,故
,故![]() x=2kπ+
x=2kπ+![]() 或2kπ+
或2kπ+![]() ,整理得x=4kπ+
,整理得x=4kπ+![]() 或x=4kπ+
或x=4kπ+![]() .
.
故解集为{x|x=4kπ+![]() 或x=4kπ+
或x=4kπ+![]() ,k∈Z}.
,k∈Z}.
(2)由于ω=1,
所以f(x)=sinx.
所以g(x)=sin2x+![]() sin(−x)sin(
sin(−x)sin(![]() −x)=
−x)=![]() sin2x=-
sin2x=-![]() sin2x−
sin2x−![]() cos2x+
cos2x+![]() =
=![]() -sin(2x+
-sin(2x+![]() ).
).
由于![]() ,
,
所以![]() ≤2x+
≤2x+![]() ≤
≤![]() .
.
![]() ≤sin(2x+
≤sin(2x+![]() )≤1,
)≤1,
故−1≤−sin(2x+![]() )≤−
)≤−![]() ,
,
故−![]() ≤g(x)≤0.
≤g(x)≤0.
所以函数g(x)的值域为![]() .
.
【考点】两角和与差的三角函数;三角函数的周期性.三角方程
【专题】转化思想;数学模型法;三角函数的求值;三角函数的图象与性质;逻辑推理;数学运算.
【分析】(1)直接利用正弦型函数的性质的应用求出结果.
(2)利用三角函数关系式的变换和正弦型函数的性质的应用求出函数的值域.
【点评】本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.
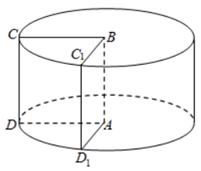
已知ABCD是边长为1的正方形,正方形ABCD绕AB旋转形成一个圆柱.
(1)求该圆柱的表面积;
(2)正方形ABCD绕AB逆时针旋转![]() 至ABC1D1,求线段CD1与平面ABCD所成的角.
至ABC1D1,求线段CD1与平面ABCD所成的角.
(1)4π (2)![]()
【解析】解:(1)该圆柱的表面由上下两个半径为1的圆面和一个长为2π、宽为1的矩形组成,
∴S=2×π×12+2π×1=4π.
故该圆柱的表面积为4π.
(2)∵正方形ABC1D1,∴AD1⊥AB,
又∠DAD1=![]() ,∴AD1⊥AD,
,∴AD1⊥AD,
∵AD∩AB=A,且AD、AB⊂平面ADB,
∴AD1⊥平面ADB,即D1在面ADB上的投影为A,
连接CD1,则∠D1CA即为线段CD1与平面ABCD所成的角,
而cos∠D1CA=![]() ,
,
∴线段CD1与平面ABCD所成的角为![]()
【考点】直线与平面所成的角.
【专题】计算题;综合题;空间角;直观想象;数学运算.
【分析】(1)该圆柱的表面由上下两个半径为1的圆面和一个长为2π、宽为1的矩形组成,依次求出圆面和矩形的面积,相加即可;
(2)先利用线面垂直的判定定理证明AD1⊥平面ADB,连接CD1,则∠D1CA即为线段CD1与平面ABCD所成的角,再利用三角函数的知识求出cos∠D1CA即可.
【点评】本题考查圆柱的表面积、空间线面夹角问题,熟练掌握线面垂直的判定定理是解题的关键,考查学生的空间立体感和运算能力,属于基础题.
在研究某市场交通情况时,道路密度是指该路段上一定时间内通过的车辆数除以时间,车辆密度是该路段一定时间内通过的车辆数除以该路段的长度,现定义交通流量为v=![]() ,x为道路密度,q为车辆密度.
,x为道路密度,q为车辆密度.
v=f(x)=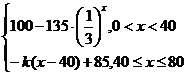 .
.
(1)若交通流量v>95,求道路密度x的取值范围;
(2)已知道路密度x=80,交通流量v=50,求车辆密度q的最大值.
(1)(3,40) (2)![]()
【解析】解:(1)∵v=![]() ,∴v越大,x越小,
,∴v越大,x越小,
∴v=f(x)是单调递减函数,k>0,
当40≤x≤80时,v最大为85,
于是只需令100−135•(![]() )x>95,解得x>3,
)x>95,解得x>3,
故道路密度x的取值范围为(3,40).
(2)把x=80,v=50代入v=f(x)=-k(x-40)+85中,
得50=-k•40+85,解得k=![]() .
.
∴q=vx=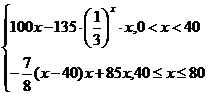 ,
,
当0<x<40时,q单调递增,q<100×40-135×(![]() )40×40≈4000;
)40×40≈4000;
当40≤x≤80时,q是关于x的二次函数,开口向下,对称轴为x=![]() ,
,
此时q有最大值,为−![]() ×(
×(![]() )2+120×
)2+120×![]() =
=![]() >4000.
>4000.
故车辆密度q的最大值为![]()
【考点】根据实际问题选择函数类型.几类不同增长的函数模型的特点
【专题】分类讨论;数学模型法;函数的性质及应用;逻辑推理.
【分析】(1)易知v越大,x越小,所以v=f(x)是单调递减函数,k>0,于是只需令100−135•(![]() )x>95,解不等式即可;
)x>95,解不等式即可;
(2)把x=80,v=50代入v=f(x)的解析式中,求出k的值,利用q=vx可得到q关于x的函数关系式,分段判断函数的单调性,并求出各自区间上q的最大值,取较大者即可.
【点评】本题考查分段函数的实际应用,考查学生分析问题和解决问题的能力,以及运算能力,属于中档题.
已知数列{an}为有限数列,满足|a1-a2|≤|a1-a3|≤…≤|a1-am|,则称{an}满足性质P.
(1)判断数列3、2、5、1和4、3、2、5、1是否具有性质P,请说明理由;
(2)若a1=1,公比为q的等比数列,项数为10,具有性质P,求q的取值范围;
(3)若{an}是1,2,3,…,m的一个排列(m≥4),{bn}符合bk=ak+1(k=1,2,…,m-1),{an}、{bn}都具有性质P,求所有满足条件的数列{an}.
见解析。
【解析】解:(1)对于数列3,2,5,1,有|2-3|=1,|5-3|=2,|1-3|=2,满足题意,该数列满足性质P;
对于第二个数列4、3、2、5、1,|3-4|=1,|2-4|=2,|5-4|=1.不满足题意,该数列不满足性质P.
(2)由题意:|a1-a1qn|≥|a1-a1qn-1|,可得:|qn-1|≥|qn-1-1|,n∈{2,3,…,9},
两边平方可得:q2n-2qn+1≥q2n-2-2qn-1+1,
整理可得:(q-1)qn-1[qn-1(q+1)-2]≥0,当q≥1时,得qn-1(q+1)-2≥0此时关于n恒成立,
所以等价于n=2时,q(q+1)-2≥0,
所以,(q+2)(q-1)≥0,所以q≤-2,或q≥1,所以取q≥1,
当0<q≤1时,得qn-1(q+1)-2≤0,此时关于n恒成立,所以等价于n=2时,q(q+1)-2≤0,
所以(q+2)(q-1)≤0,所以-2≤q≤1,所以取0<q≤1.
当-1≤q<0时:qn-1[qn-1(q+1)-2]≤0,
当n为奇数时,得qn-1(q+1)-2≤0,恒成立,当n为偶数时,qn-1(q+1)-2≥0,不恒成立;
故当-1≤q<0时,矛盾,舍去.
当q<-1时,得qn-1[qn-1(q+1)-2]≤0,当n为奇数时,得qn-1(q+1)-2≤0,恒成立,
当n为偶数时,qn-1(q+1)-2≥0,恒成立;故等价于n=2时,q(q+1)-2≥0,
所以(q+2)(q-1)≥0,所以q≤-2或q≥1,所以取q≤-2,
综上q∈(-∞,-2]∪(0,+∞).
(3)设a1=p,p∈{3,4,…,m-3,m-2},
因为a1=p,a2可以取p-1,或p+1,a3可以取p-2,或p+2,
如果a2或a3取了p-3或p+3,将使{an}不满足性质P;所以{an}的前5项有以下组合:
①a1=p,a2=p-1;a3=p+1;a4=p-2;a5=p+2;
②a1=p,a2=p-1;a3=p+1;a4=p+2;a5=p-2;
③a1=p,a2=p+1;a3=p-1;a4=p-2;a5=p+2;
④a1=p,a2=p+1;a3=p-1;a4=p+2;a5=p-2;
对于①,b1=p-1,|b2-b1|=2,|b3-b1|=1,与{bn}满足性质P矛盾,舍去;
对于②,b1=p-1,|b2-b1|=2,|b3-b1|=3,|b4-b1|=2与{bn}满足性质P矛盾,舍去;
对于③,b1=p+1,|b2-b1|=2,|b3-b1|=3,|b4-b1|=1与{bn}满足性质P矛盾,舍去;
对于④b1=p+1,|b2-b1|=2,|b3-b1|=1,与{bn}满足性质P矛盾,舍去;
所以P∈{3,4,…,m-3,m-2},均不能同时使{an}、{bn}都具有性质P.
当p=1时,有数列{an}:1,2,3,…,m-1,m满足题意.
当p=m时,有数列{an}:m,m-,…,3,2,1满足题意.
当p=2时,有数列{an}:2,1,3,…,m-1,m满足题意.
当p=m-1时,有数列{an}:m-1,m,m-2,m-3,…,3,2,1满足题意.
所以满足题意的数列{an}只有以上四种.
【考点】数列的应用;等差数列与等比数列的综合.等比数列的实际应用
【专题】计算题;转化思想;分析法;函数的性质及应用;等差数列与等比数列;数学运算.
【分析】(1)根据定义,验证两个数列3、2、5、1和4、3、2、5、1是否具有性质P即可;
(2)假设公比q的等比数列满足性质p,可得:|a1-a1qn|≥|a1-a1qn-1|,推出(q-1)qn-1(qn-1(q+1)-2)≥0,通过q≥1,0<q≤1时,-1≤q<0时:q<-1时,四种情况讨论求解即可.
(3)设a1=p,分p=1时,当p=m时,当p=2时,当p=m-1时,以及P∈{3,4,…,m-3,m-2},五种情况讨论,判断数列{an}的可能情况,分别推出{bn}判断是否满足性质P即可.
【点评】本题考查数列的综合应用,不等式以及不等关系,二次函数的性质以及函数的相关性质的综合应用,考查分析问题解决问题的能力是难度大的题目,必须由高的数学思维逻辑修养才能解答.
本卷还有16题,登录并加入会员即可免费使用哦~

该作品由: 用户青春无悔分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。