已知圆C经过A(﹣2,0),B(1,![]() )两点,且圆心C在直线l1:y=x上.
)两点,且圆心C在直线l1:y=x上.
(1)求圆C的方程;
(2)已知过点P(1,2)的直线l2与圆C相交截得的弦长为![]() ,求直线l2的方程;
,求直线l2的方程;
(3)已知点M(1,1),在平面内是否存在异于点M的定点N,对于圆C上的任意动
点Q,都有![]() 为定值?若存在求出定点N的坐标,若不存在说明理由.
为定值?若存在求出定点N的坐标,若不存在说明理由.
解:(1)因为圆C经过A(﹣2,0),B(1,![]() )两点,且圆心C在直线l1:y=x上,
)两点,且圆心C在直线l1:y=x上,
设圆C:x2+y2+Dx+Ey+F=0,
所以(﹣2)2﹣2D+F=0,12+(![]() )2+D+E+F=0,﹣
)2+D+E+F=0,﹣![]() =﹣
=﹣![]() ,
,
所以D=E=0,F=﹣4.
所以圆C:x2+y2=4.
(2)当斜率不存在的时候,x=1,弦长为2![]() ,满足题意;
,满足题意;
当斜率存在的时候,设l2:y﹣2=k(x﹣1),即kx﹣y+2﹣k=0,
![]() =1,k=
=1,k=![]() ,
,
所以直线l2的方程为:x=1或3x﹣4y+5=0.
(3)设Q(x0,y0),N(m,n),且x02+y02=4.
![]() =
=![]() =
=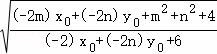 ,
,
因为![]() 为定值,设
为定值,设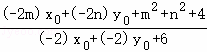 =λ,
=λ,
化简得:(2λ﹣2m)x0+(2λ﹣2n)y0+m2+n2+4﹣6λ=0,与Q点位置无关,
所以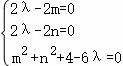 ,
,
解得m=n=1或m=n=2.
所以定点为(2,2).
如图,OPQ是半径为2,圆心角为![]() 的扇形,点A在弧
的扇形,点A在弧![]() 上(异于点P,Q),过点
上(异于点P,Q),过点
A作AB⊥OP,AC⊥OQ,垂足分别为B,C,记∠AOB=![]() ,四边形ACOB的面积为S.
,四边形ACOB的面积为S.
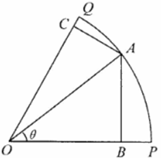
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,S有最大值,并求出这个最大值.
为何值时,S有最大值,并求出这个最大值.
解:(1)因为AB⊥OP,所以在Rt△OAB中,AB=OAsinθ=2sinθ,OB=OAcosθ=2cosθ,
![]() ,
,
因为![]() ,所以
,所以![]() ;
;
同理:![]() ;
;
从而S关于θ的解析式为
S=S△ABO+S△ACO=sin2θ+sin(![]() ﹣2θ),(0<θ<
﹣2θ),(0<θ<![]() );(不写定义域扣分)
);(不写定义域扣分)
(2)化简函数![]()
=![]()
=![]()
=![]()
=![]()
=![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故当![]() ,即
,即![]() 时S有最大值,最大值为
时S有最大值,最大值为![]() .
.
答:当θ为![]() 时,面积S有最大值,最大值为
时,面积S有最大值,最大值为![]() .
.
如图,在三棱锥![]() 中,平面
中,平面![]() ⊥平面
⊥平面![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]()
的中点.
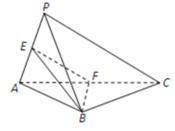
求证:(1)![]() ∥平面
∥平面![]() (2)平面
(2)平面![]() ⊥平面
⊥平面![]() .
.
证明:(1)在△APC中,因为E,F分别是PA,AC的中点,
所以EF∥PC,
又PC⊂平面PAC,EF⊄平面PAC,
所以EF∥平面PBC;
(2)因为AB=BC,且点F是AC的中点,
所以BF⊥AC,
又平面ABC⊥平面PAC,平面ABC∩平面PAC=AC,BF⊂平面ABC,
所以BF⊥平面PAC,
因为EF⊂平面BEF,
所以平面BEF⊥平面PAC.
已知α∈![]() ,且
,且![]() .
.
(1)求cos α的值;(2)若sin(α-β)=-![]() ,β∈
,β∈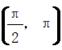 ,求cos β的值.
,求cos β的值.
解:(1)∵α∈(![]() ,π),且sin
,π),且sin![]() +cos
+cos![]() =
=![]() ,两边平方可得:1+sinα=
,两边平方可得:1+sinα=![]() ,∴sinα=
,∴sinα=![]() ,可得:cosα=﹣
,可得:cosα=﹣![]() =﹣
=﹣![]() .
.
(2)∵由(1)可得:sin α=![]() ,cosα=﹣
,cosα=﹣![]() .
.
∵![]() <α<π,
<α<π,![]() <β<π,∴﹣
<β<π,∴﹣![]() <α﹣β<
<α﹣β<![]() ,
,
又sin(α﹣β)=﹣![]() ,得cos(α﹣β)=
,得cos(α﹣β)=![]() ,
,
∴cos β=cos[α﹣(α﹣β)]=cosαcos(α﹣β)+sinαsin(α﹣β)=﹣![]() ×
×![]() +
+![]() ×(﹣
×(﹣![]() )=﹣
)=﹣![]() .
.
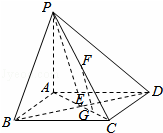
如图,四棱锥P—ABCD中,底面ABCD为菱形,PA⊥平面ABCD,BD交AC于点E,F
是线段PC中点,G为线段EC中点.
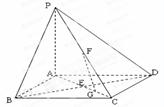
(1)求证:FG//平面PBD;
(2)求证:BD⊥FG.
证明:(Ⅰ)连接PE,G、F为EC和PC的中点,
∴FG∥PE,FG⊄平面PBD,PE⊂平面PBD,
∴FG∥平面PBD
(Ⅱ)∵菱形ABCD,∴BD⊥AC,
又PA⊥面ABCD,BD⊂平面ABCD,
∴BD⊥PA,
∵PA⊂平面PAC,AC⊂平面PAC,且PA∩AC=A,
∴BD⊥平面PAC,FG⊂平面PAC,
∴BD⊥FG
本卷还有17题,登录并加入会员即可免费使用哦~

该作品由: 用户高文臣分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。