
-
难度:




 使用次数:121
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:121
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析已知椭圆C的离心率为
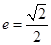 ,长轴的左、右端点分别为
,长轴的左、右端点分别为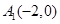 ,
,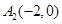 .
.
(1)求椭圆C的方程;
(2)设直线
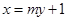 与椭圆C交于P,Q两点,直线
与椭圆C交于P,Q两点,直线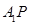 ,
, 交于S,试问:当m变化时,点S是否恒在一条定直线上?若是,请写出这条直线的方程,并证明你的结论;若不是,请说明理由.题型:解答题 知识点:1.2圆锥曲线与方程
交于S,试问:当m变化时,点S是否恒在一条定直线上?若是,请写出这条直线的方程,并证明你的结论;若不是,请说明理由.题型:解答题 知识点:1.2圆锥曲线与方程 -
难度:




 使用次数:292
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:292
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析已知椭圆
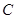 :
: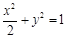 的左、右焦点分别为
的左、右焦点分别为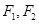 ,下顶点为
,下顶点为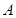 ,点
,点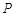 是椭圆上任一点,⊙
是椭圆上任一点,⊙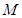 是以
是以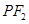 为直径的圆.
为直径的圆. 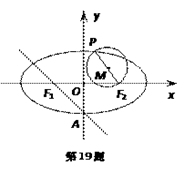
(Ⅰ)当⊙
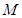 的面积为
的面积为 时,求
时,求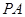 所在直线的方程;
所在直线的方程;(Ⅱ)当⊙
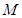 与直线
与直线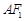 相切时,求⊙
相切时,求⊙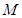 的方程;
的方程;(Ⅲ)求证:⊙
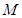 总与某个定圆相切. 题型:解答题 知识点:第四章圆与方程
总与某个定圆相切. 题型:解答题 知识点:第四章圆与方程 -
难度:




 使用次数:121
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:121
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析如图所示,在五棱锥
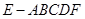 中,侧面
中,侧面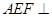 底面
底面 ,
,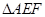 是边长为2的正三角形,四边形
是边长为2的正三角形,四边形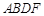 为正方形,
为正方形,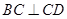 ,且
,且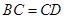 ,
,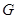 是
是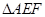 的重心,
的重心,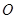 是正方形
是正方形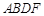 的中心.
的中心.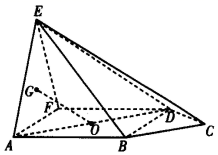
(Ⅰ)求证:
 平面
平面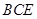 ;
;(Ⅱ)求二面角
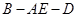 的余弦值.题型:解答题 知识点:第二章点、直线、平面之间的位置
的余弦值.题型:解答题 知识点:第二章点、直线、平面之间的位置 -
难度:




 使用次数:277
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:277
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析已知圆心在
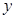 轴上的圆
轴上的圆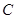 经过点
经过点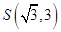 ,截直线
,截直线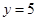 所得弦长为
所得弦长为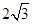 ,直线
,直线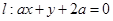 .
.(1)求圆
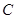 的方程;
的方程;(2)若直线
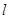 与圆
与圆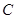 相交于
相交于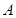 、
、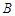 两点,当
两点,当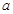 为何值时,
为何值时, 的面积最大.题型:解答题 知识点:第四章圆与方程
的面积最大.题型:解答题 知识点:第四章圆与方程 -
难度:




 使用次数:227
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:227
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,
 ,
,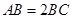 ,
,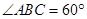 ,
,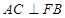 .
.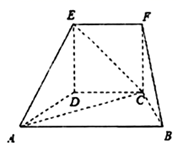
(1)求证:
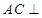 平面FBC;
平面FBC;(2)线段ED上是否存在点Q,使平面
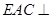 平面QBC?证明你的结论.题型:解答题 知识点:第二章点、直线、平面之间的位置
平面QBC?证明你的结论.题型:解答题 知识点:第二章点、直线、平面之间的位置 -
难度:




 使用次数:227
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:227
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析求满足下列条件的双曲线的标准方程:
(1)一条渐近线方程为
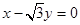 ,且与椭圆
,且与椭圆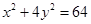 有相同的焦点;
有相同的焦点;(2)经过点
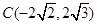 ,且与双曲线
,且与双曲线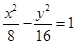 有共同的渐近线.题型:解答题 知识点:1.2圆锥曲线与方程
有共同的渐近线.题型:解答题 知识点:1.2圆锥曲线与方程 -
难度:




 使用次数:199
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:199
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析如图,平面
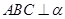 ,D为AB的中点,
,D为AB的中点,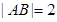 ,
,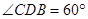 ,P为
,P为 内的动点,且P到直线CD的距离为
内的动点,且P到直线CD的距离为 ,则
,则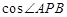 的最小值为________.
的最小值为________.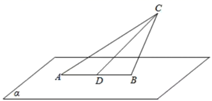 题型:填空题 知识点:1.2圆锥曲线与方程
题型:填空题 知识点:1.2圆锥曲线与方程 -
难度:




 使用次数:127
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:127
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析直线
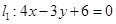 和直线
和直线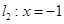 ,抛物线
,抛物线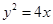 上一动点
上一动点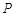 到直线
到直线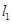 和直线
和直线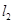 的距离之和的最小值是_____________.题型:填空题 知识点:第二章 基本初等函数I
的距离之和的最小值是_____________.题型:填空题 知识点:第二章 基本初等函数I -
难度:




 使用次数:181
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:181
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析已知正四棱锥
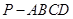 中,
中,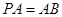 ,E,F分别是PB,PC的中点,则异面直线AE与BF所成角的余弦值为________.
,E,F分别是PB,PC的中点,则异面直线AE与BF所成角的余弦值为________. 题型:填空题 知识点:2.3空间中的向量与立体几何
题型:填空题 知识点:2.3空间中的向量与立体几何 -
难度:




 使用次数:103
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:103
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析直线
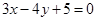 关于直线
关于直线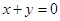 对称的直线方程为________.题型:填空题 知识点:第三章直线与方程
对称的直线方程为________.题型:填空题 知识点:第三章直线与方程 -
难度:




 使用次数:251
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:251
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析已知双曲线
 的两条渐近线分别与抛物线
的两条渐近线分别与抛物线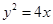 交于第一、四象限的A,B两点,设抛物线焦点为F,若
交于第一、四象限的A,B两点,设抛物线焦点为F,若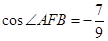 ,则双曲线的离心率为( )
,则双曲线的离心率为( )A.
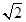 B.
B. C.
C.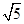 D.
D.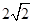 题型:选择题 知识点:第一章三角函数
题型:选择题 知识点:第一章三角函数 -
难度:




 使用次数:246
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:246
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析如图,等边
 的中线
的中线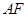 与中位线
与中位线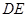 相交于
相交于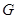 ,已知
,已知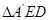 是
是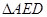 绕
绕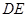 旋转过程中的一个图形,下列命题中,错误的是( )
旋转过程中的一个图形,下列命题中,错误的是( )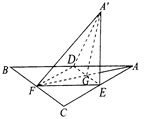
A.动点
 在平面
在平面 上的射影在线段
上的射影在线段 上
上B.恒有平面
 ⊥平面
⊥平面
C.三棱锥
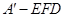 的体积有最大值
的体积有最大值D.异面直线
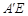 与
与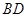 不可能垂直题型:选择题 知识点:第一章空间几何体
不可能垂直题型:选择题 知识点:第一章空间几何体 -
难度:




 使用次数:186
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:186
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析正四面体ABCD的体积为1,O为其中心,正四面体EFGH与正四面体ABCD关于点O对称,则这两个正四面体的公共部分的体积为( )
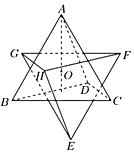
A.
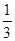 B.
B.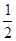 C.
C.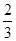 D.
D.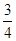 题型:选择题 知识点:第一章空间几何体
题型:选择题 知识点:第一章空间几何体 -
难度:




 使用次数:129
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:129
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析如图,过抛物线
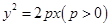 的焦点F的直线依次交抛物线及准线于点A,B,C,若
的焦点F的直线依次交抛物线及准线于点A,B,C,若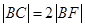 ,且
,且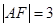 ,则抛物线的方程为( )
,则抛物线的方程为( )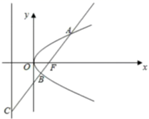
A.
 B.
B.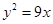 C.
C.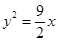 D.
D. 题型:选择题 知识点:1.2圆锥曲线与方程
题型:选择题 知识点:1.2圆锥曲线与方程 -
难度:




 使用次数:249
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:249
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析在棱长为2的正方体ABCD-A1B1C1D1中,点P,Q,R分别为棱AA1,BC,C1D1的中点,经过P,Q,R三点的平面为
 ,平面
,平面 被此正方体所截得截面图形的面积为( )
被此正方体所截得截面图形的面积为( )A.
 B.
B. C.
C.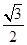 D.
D.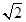 题型:选择题 知识点:第一章空间几何体
题型:选择题 知识点:第一章空间几何体 -
难度:




 使用次数:243
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:243
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析如图所示,点
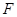 是抛物线
是抛物线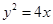 的焦点,点
的焦点,点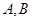 分别在抛物线
分别在抛物线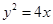 及圆
及圆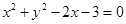 的实线部分上运动,且
的实线部分上运动,且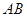 总是平行于
总是平行于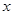 轴,则
轴,则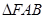 的周长的取值范围( )
的周长的取值范围( )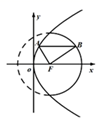
A.
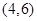 B.
B.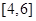 C.
C.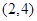 D.
D.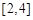 题型:选择题 知识点:1.2圆锥曲线与方程
题型:选择题 知识点:1.2圆锥曲线与方程 -
难度:




 使用次数:150
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:150
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析一个几何体的三视图如图所示,其体积为( )
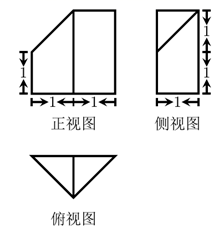
A.
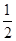 B.
B.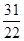 C.
C.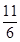 D.
D.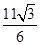 题型:选择题 知识点:第一章空间几何体
题型:选择题 知识点:第一章空间几何体 -
难度:




 使用次数:160
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:160
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析某正三棱柱各棱长均为
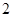 ,则该棱柱的外接球表面积为( )
,则该棱柱的外接球表面积为( )A.
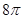 B.
B. C.
C.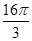 D.
D.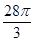 题型:选择题 知识点:第一章空间几何体
题型:选择题 知识点:第一章空间几何体 -
难度:




 使用次数:128
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:128
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析在平面直角坐标系xOy中,椭圆
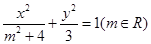 的离心率的取值范围为( )
的离心率的取值范围为( )A.
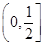 B.
B.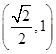 C.
C.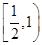 D.
D.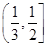 题型:选择题 知识点:1.2圆锥曲线与方程
题型:选择题 知识点:1.2圆锥曲线与方程 -
难度:




 使用次数:131
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析
使用次数:131
入库时间:2021-01-22来源: 安徽省合肥市庐阳区第一中学2019-2020学年高二上学期期末考试理科数学试题含答案解析一条光线从点
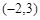 射出,经
射出,经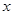 轴反射后与圆
轴反射后与圆 相切,则反射光线所在直线的斜率为( )
相切,则反射光线所在直线的斜率为( )A.
 或
或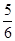 B.
B.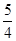 或
或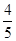 C.
C.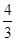 或
或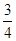 D.
D.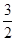 或
或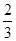 题型:选择题 知识点:第四章圆与方程
题型:选择题 知识点:第四章圆与方程