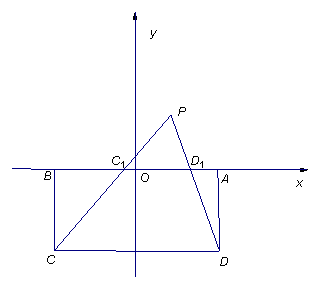
如图, 矩形![]() 中,
中, ![]() ,
, ![]() , 现以矩形
, 现以矩形![]() 的
的![]() 边为
边为![]() 轴,
轴, ![]() 的中点
的中点
为原点建立直角坐标系, ![]() 是
是![]() 轴上方一点, 使得
轴上方一点, 使得![]() 、
、![]() 与线段
与线段![]() 分别交于点
分别交于点![]() 、
、![]() ,
,
 且
且![]() 成等比数列.
成等比数列.
(1) 求动点![]() 的轨迹方程;
的轨迹方程;
(2) 求动点![]() 到直线
到直线![]()
![]() 距离
距离
的最大值及取得最大值时点![]() 的坐标.
的坐标.
答案
解:(1)设点![]() 的坐标为
的坐标为![]()
![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,交
,交![]() 的延
的延
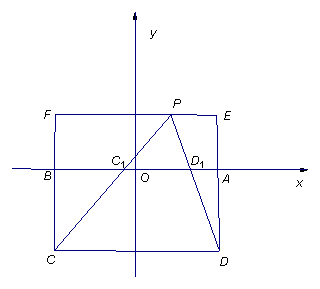 长线于
长线于![]() .
.
在![]() 中,
中, ![]() , 得
, 得![]() ,
,
得![]() .
.
在![]() 中,
中, ![]()
![]() ,
,
得![]() .
.
 同理可得
同理可得![]() .
.
∵ ![]() 成等比数列,
成等比数列,
∴ ![]() .
.
∴ 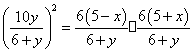 .
.
化简得![]() .
.
∴ 动点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)由图易知当与直线![]() 平行的直线与半椭圆相切于点
平行的直线与半椭圆相切于点![]() 时,点
时,点![]() 到直线
到直线![]() 距离的最大.
距离的最大.
设与直线![]()
![]() 平行的直线方程为
平行的直线方程为![]() ,代入
,代入![]() ,
,
得 ![]() ,①
,①
由![]() ,
,
解得![]() ,由
,由![]() ,得
,得![]() .
.
故点![]() 到直线
到直线![]() 距离的最大值为
距离的最大值为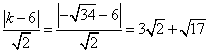 .
.
把![]() 代入①式,可解得点
代入①式,可解得点![]() 的坐标为
的坐标为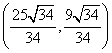 .
.
