若数列![]() 满足
满足![]() ,且存在常数
,且存在常数![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() ,则称数列
,则称数列![]() 为“k控数列”.
为“k控数列”.
(1)若公差为d的等差数列![]() 是“2控数列”,求d的取值范围;
是“2控数列”,求d的取值范围;
(2)已知公比为![]() 的等比数列
的等比数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 与
与![]() 都是“k控数列”,求q的取值范围(用k表示).
都是“k控数列”,求q的取值范围(用k表示).
答案
(1)![]() (2)
(2)![]() .
.
【分析】
(1)根据“![]() 控数列”的定义得出
控数列”的定义得出![]() ,则由等差数列的通项公式可得
,则由等差数列的通项公式可得![]() 对
对![]() 恒成立,求出公差
恒成立,求出公差![]() 的取值范围;
的取值范围;
(2)由等比数列![]() 为“
为“![]() 控数列”得
控数列”得![]() ,又
,又![]() 是“
是“![]() 控数列”得
控数列”得![]() ,分类讨论求出q的取值范围.
,分类讨论求出q的取值范围.
【详解】
(1)因为公差为![]() 的等差数列
的等差数列![]() 是“2控数列”,所以
是“2控数列”,所以![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以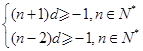
由![]() 得所以
得所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
由![]() 得:
得:
当![]() 时,
时,![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() 成立;
成立;
当![]() 时,
时,![]() ,又
,又![]() ,所以
,所以![]() ;
;
综上,![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() ;
;
(2)因为数列![]() 是公比为
是公比为![]() 的等比数列且为“
的等比数列且为“![]() 控数列”,所以
控数列”,所以![]() ,显然
,显然![]() ,故
,故![]() .
.
易知![]() ,要使
,要使![]() 是“
是“![]() 控数列”,
控数列”,
则![]() ,
,
(ⅰ)当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]() 递减,
递减,
所以![]() ,
,
所以![]() ,即
,即![]() .
.
要使![]() 存在,则
存在,则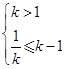 得
得![]() ;
;
(ⅱ)当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]() 递减,
递减,![]() ,
,
所以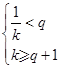 ,又
,又![]() ,所以
,所以![]() ,
,
要使![]() 存在,需
存在,需![]() ,得
,得![]()
综上,当![]() 时,公比
时,公比![]() 的取值范围是
的取值范围是![]() .
.
【点睛】
本题主要考查等差数列的通项公式、等比数列的前![]() 项和公式,数列不等式的恒成立问题,考查了分类讨论的思想,考查了学生的逻辑推理与运算求解能力.
项和公式,数列不等式的恒成立问题,考查了分类讨论的思想,考查了学生的逻辑推理与运算求解能力.

 ,简记为数列{an},其中数列的第一项a1也称首项,an是数列的第n项,也叫数列的通项2
,简记为数列{an},其中数列的第一项a1也称首项,an是数列的第n项,也叫数列的通项2