如图,设A是由![]() 个实数组成的n行n列的数表,其中aij (i,j=1,2,3,…,n)表示位于第i行第j列的实数,且aij
个实数组成的n行n列的数表,其中aij (i,j=1,2,3,…,n)表示位于第i行第j列的实数,且aij![]() {1,-1}.记S(n,n)为所有这样的数表构成的集合.对于
{1,-1}.记S(n,n)为所有这样的数表构成的集合.对于![]() ,记ri (A)为A的第i行各数之积,cj (A)为A的第j列各数之积.令
,记ri (A)为A的第i行各数之积,cj (A)为A的第j列各数之积.令![]()
| a11 | a12 | … | a1n |
| a21 | a22 | a2n | |
| … | … | … | … |
| an1 | an2 | … | ann |
(Ⅰ)请写出一个A![]() S(4,4),使得l(A)=0;
S(4,4),使得l(A)=0;
(Ⅱ)是否存在A![]() S(9,9),使得l(A)=0?说明理由;
S(9,9),使得l(A)=0?说明理由;
(Ⅲ)给定正整数n,对于所有的A![]() S(n,n),求l(A)的取值集合.
S(n,n),求l(A)的取值集合.
答案
(Ⅰ)答案见解析;(Ⅱ)不存在,理由见解析;(Ⅲ)![]()
【分析】
(Ⅰ)可取第一行都为-1,其余的都取1,即满足题意;
(Ⅱ)用反证法证明:假设存在,得出矛盾,从而证明结论;
(Ⅲ)通过分析正确得出l(A)的表达式,以及从A0如何得到A1,A2……,以此类推可得到Ak.
【详解】
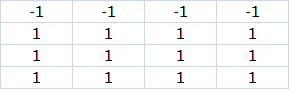
(Ⅰ)答案不唯一,如图所示数表符合要求.
(Ⅱ)不存在A![]() S(9,9),使得l(A)=0,证明如下:
S(9,9),使得l(A)=0,证明如下:
假如存在![]() ,使得
,使得![]() .
.
因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,...,
,...,![]() ,
,![]() ,
,![]() ,...,
,...,![]() 这18个数中有9个1,9个-1.
这18个数中有9个1,9个-1.
令![]() .
.
一方面,由于这18个数中有9个1,9个-1,从而![]() ①,
①,
另一方面,![]() 表示数表中所有元素之积(记这81个实数之积为m);
表示数表中所有元素之积(记这81个实数之积为m);
![]() 也表示m,从而
也表示m,从而![]() ②,
②,
①,②相矛盾,从而不存在![]() ,使得
,使得![]() .
.
(Ⅲ)记这![]() 个实数之积为p.
个实数之积为p.
一方面,从“行”的角度看,有![]() ;
;
另一方面,从“列”的角度看,有![]() ;
;
从而有![]() ③,
③,
注意到![]() ,
,![]() ,
,
下面考虑![]() ,
,![]() ,...,
,...,![]() ,
,![]() ,
,![]() ,...,
,...,![]() 中-1的个数,
中-1的个数,
由③知,上述2n个实数中,-1的个数一定为偶数,该偶数记为![]() ,则1的个数为2n-2k,
,则1的个数为2n-2k,
所以![]() ,
,
对数表![]() ,显然
,显然![]() .
.
将数表![]() 中的
中的![]() 由1变为-1,得到数表
由1变为-1,得到数表![]() ,显然
,显然![]() ,
,
将数表![]() 中的
中的![]() 由1变为-1,得到数表
由1变为-1,得到数表![]() ,显然
,显然![]() ,
,
依此类推,将数表![]() 中的
中的![]() 由1变为-1,得到数表
由1变为-1,得到数表![]() ,
,
即数表![]() 满足:
满足:![]() ,其余
,其余![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
由k的任意性知,l(A)的取值集合为![]() .
.
【点睛】
本题为数列的创新应用题,考查数学分析与思考能力及推理求解能力,解题关键是读懂题意,根据引入的概念与性质进行推理求解,属于较难题.

 ,简记为数列{an},其中数列的第一项a1也称首项,an是数列的第n项,也叫数列的通项2
,简记为数列{an},其中数列的第一项a1也称首项,an是数列的第n项,也叫数列的通项2