A

【分析】由直线 经过函数 图象相邻的一个最高点和一个最低点，可知交点的坐标分别为 和 ，借助草图可知函数 的周期，进而可求出 的解析式，从而可得 的值 .

【详解】由题意，得 的图象经过点 和 ，则最小正周期为 ，故 .

由 的图像经过点 ，得 ， ，则 ， .

又 ， ，所以 ，故 .

故选： A

B

【分析】将函数进行化简，结合三角函数的图像和性质即可求函数 图像的单调区间、对称轴、平移、值域．

【详解】 ，

求函数的单调减区间：由 ，得 ，

时，有 在区间 上是减函数， ① 正确；

求函数的对称轴：由 ，得 ，

时， 是函数 图像的一条对称轴 ， ② 正确；

由 向左平移 个单位后得到 ， ③ 不正确；

当 时， ，有 ，所以 的值域为 ， ④ 不正确．

故正确的是 ①② ，正确的命题个数是 2 个 .

故选： B

A

【分析】通过函数 的平移变换后图象关于直线 对称可求得 值，从而可求出函数解析式，然后使用换元法画出函数图象，再逐项判断即可 .

【详解】函数 ， 图象向左平移 个单位后的图象对应的解析式为： ；

而 图象关于直线 对称，且 ，于是 ， ；

；

，所以 不关于 对称，故 B 错误；

当 时，则 ，令 ，则 ，此时函数图象如图 :

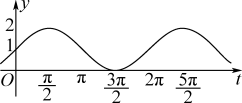
结合图象可知，当 时，即 ， 与坐标轴只有一个交点，即 只有一个零点，故 A 正确；

当 时，则 ，结合图象可知，此时 有增有减，故 C 错误；

当 时，则 ，结合图象可知，此时 单调递增，所以，当 时，即 ，函数取最大值， ，故 D 错误；

故选： A.

A

【分析】 ， 再求出平移后的解析式，由其为偶函数，由两角和与差的正弦公式展开后由三角函数的性质可求得的 m 值，从而得到最小值．

【详解】 ，

图像向左平移 个单位后得到 ，

由函数为偶函数 ，

有 ，

∴ ，

得 ，

∴ ，

∴ ， ，

即 ． ，

由 ，所以当 时， m 的最小值 为 ．

故选 ： A

C

【分析】根据三角函数的性质，利用整体思想，由单调区间与周期的关系，根据零点与对称轴之间的距离，表示所求参数，逐个检验取值，可得答案 .

【详解】由 f （ x ）在 上单调，即 ，可得 ，则 ω ≤9 ；

∵ 为 f （ x ）的零点， 为 y ＝ f （ x ）图象的对称轴，

根据三角函数的图象可知，零点与对称轴之间距离为： ， k ∈ N * ．

要求 最大，则周期最小， ∴ ，则 T ； ∴ ω ＝ 2 k ﹣ 1 ；

当 时，由 ，则 ，可得 ，

易知 在 上单减，在 上递增，不合题意；

当 时，由 ，则 ，可得 ，

易知 在 上单减，在 上递增，不合题意；

当 时，由 ，则 ，可得 ，

易知 在 上单减，符合题意；

故选： C ．