如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
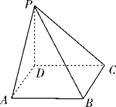
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
(1)证明见解析;(2)![]() .
.
【解析】
【分析】
(1)利用线面垂直的判定定理证得![]() 平面
平面![]() ,利用线面平行的判定定理以及性质定理,证得
,利用线面平行的判定定理以及性质定理,证得![]() ,从而得到
,从而得到![]() 平面
平面![]() ;
;
(2)根据题意,建立相应的空间直角坐标系,得到相应点的坐标,设出点![]() ,之后求得平面
,之后求得平面![]() 的法向量以及向量
的法向量以及向量![]() 的坐标,求得
的坐标,求得![]() 的最大值,即为直线
的最大值,即为直线![]() 与平面
与平面![]() 所成角的正弦值的最大值.
所成角的正弦值的最大值.
【详解】(1)证明:
在正方形![]() 中,
中,![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() ,
,
因为在四棱锥![]() 中,底面
中,底面![]() 是正方形,所以
是正方形,所以![]()
且![]() 平面
平面![]() ,所以
,所以![]()
因为![]()
所以![]() 平面
平面![]() ;
;
(2)如图建立空间直角坐标系![]() ,
,
因为![]() ,则有
,则有![]() ,
,
设![]() ,则有
,则有![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则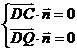 ,即
,即![]() ,
,
令![]() ,则
,则![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
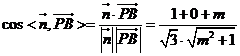
根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,所以直线与平面所成角的正弦值等于![]()
![]()
![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以直线![]() 与平面
与平面![]() 所成角的正弦值的最大值为
所成角的正弦值的最大值为![]() .
.
【点睛】该题考查的是有关立体几何的问题,涉及到的知识点有线面平行的判定和性质,线面垂直的判定和性质,利用空间向量求线面角,利用基本不等式求最值,属于中档题目.
为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了![]() 天空气中的
天空气中的![]() 和
和![]() 浓度(单位:
浓度(单位:![]() ),得下表:
),得下表:
|
|
|
|
|
|
| 32 | 18 | 4 |
|
| 6 | 8 | 12 |
|
| 3 | 7 | 10 |
(1)估计事件“该市一天空气中![]() 浓度不超过
浓度不超过![]() ,且
,且![]() 浓度不超过
浓度不超过![]() ”的概率;
”的概率;
(2)根据所给数据,完成下面的![]() 列联表:
列联表:
|
|
|
|
|
| ||
|
|
(3)根据(2)中的列联表,判断是否有![]() 的把握认为该市一天空气中
的把握认为该市一天空气中![]() 浓度与
浓度与![]() 浓度有关?
浓度有关?
附: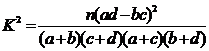 ,
,
|
| 0.050 0.010 0.001 |
|
| 3.841 6.635 10.828 |
(1)![]() ;(2)答案见解析;(3)有.
;(2)答案见解析;(3)有.
【解析】
【分析】
(1)根据表格中数据以及古典概型的概率公式可求得结果;
(2)根据表格中数据可得![]() 列联表;
列联表;
(3)计算出![]() ,结合临界值表可得结论.
,结合临界值表可得结论.
【详解】(1)由表格可知,该市100天中,空气中的![]() 浓度不超过75,且
浓度不超过75,且![]() 浓度不超过150的天数有
浓度不超过150的天数有![]() 天,
天,
所以该市一天中,空气中的![]() 浓度不超过75,且
浓度不超过75,且![]() 浓度不超过150的概率为
浓度不超过150的概率为![]() ;
;
(2)由所给数据,可得![]() 列联表为:
列联表为:
|
|
|
| 合计 |
|
| 64 | 16 | 80 |
|
| 10 | 10 | 20 |
| 合计 | 74 | 26 | 100 |
(3)根据![]() 列联表中的数据可得
列联表中的数据可得
![]()
![]() ,
,
因为根据临界值表可知,有![]() 的把握认为该市一天空气中
的把握认为该市一天空气中![]() 浓度与
浓度与![]() 浓度有关.
浓度有关.
【点睛】本题考查了古典概型的概率公式,考查了完善![]() 列联表,考查了独立性检验,属于中档题.
列联表,考查了独立性检验,属于中档题.
已知公比大于![]() 的等比数列
的等比数列![]() 满足
满足![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)记![]() 为
为![]() 在区间
在区间![]() 中的项的个数,求数列
中的项的个数,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(1)![]() ;(2)
;(2)![]() .
.
【解析】
【分析】
(1)利用基本元的思想,将已知条件转化为![]() 的形式,求解出
的形式,求解出![]() ,由此求得数列
,由此求得数列![]() 的通项公式.
的通项公式.
(2)通过分析数列![]() 的规律,由此求得数列
的规律,由此求得数列![]() 的前
的前![]() 项和
项和![]() .
.
【详解】(1)由于数列![]() 是公比大于
是公比大于![]() 的等比数列,设首项为
的等比数列,设首项为![]() ,公比为
,公比为![]() ,依题意有
,依题意有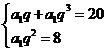 ,解得
,解得![]() ,所以
,所以![]() ,所以数列
,所以数列![]() 的通项公式为
的通项公式为![]() .
.
(2)由于![]() ,所以
,所以
![]() 对应的区间为:
对应的区间为:![]() ,则
,则![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() ;
;
![]() 对应的区间分别为:
对应的区间分别为:![]() ,则
,则![]() ,即有
,即有![]() 个
个![]() .
.
所以![]() .
.
【点睛】本小题主要考查等比数列基本量的计算,考查分析思考与解决问的能力,属于中档题.
在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求
这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求![]() 的值;若问题中的三角形不存在,说明理由.
的值;若问题中的三角形不存在,说明理由.
问题:是否存在![]() ,它的内角
,它的内角![]() 的对边分别为
的对边分别为![]() ,且
,且![]() ,
,![]() ,________?
,________?
注:如果选择多个条件分别解答,按第一个解答计分.
详见解析
【解析】
【分析】
由题意结合所给的条件首先设出a,b的长度,然后结合余弦定理和正弦定理解三角形确定边长c即可.
【详解】选择条件①的解析:
由![]() 可得:
可得:![]() ,
,
不妨设![]() ,
,
则:![]() ,即
,即![]() .
.
据此可得:![]() ,
,![]() ,此时
,此时![]() .
.
选择条件②的解析:
由![]() 可得:
可得:![]() ,
,
不妨设![]() ,
,
则:![]() ,即
,即![]() .
.
据此可得:![]() ,
,
则: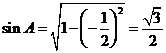 ,此时:
,此时:![]() ,则:
,则:![]() .
.
选择条件③的解析:
由![]() 可得:
可得:![]() ,
,
不妨设![]() ,
,
则:![]() ,即
,即![]() .
.
据此可得![]() ,
,![]() ,
,
与条件![]() 矛盾,则问题中的三角形不存在.
矛盾,则问题中的三角形不存在.
【点睛】在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.应用正、余弦定理时,注意公式变式的应用.解决三角形问题时,注意角的限制范围.
某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A. 62% B. 56%
C. 46% D. 42%
C
【解析】
【分析】
记“该中学学生喜欢足球”为事件![]() ,“该中学学生喜欢游泳”为事件
,“该中学学生喜欢游泳”为事件![]() ,则“该中学学生喜欢足球或游泳”为事件
,则“该中学学生喜欢足球或游泳”为事件![]() ,“该中学学生既喜欢足球又喜欢游泳”为事件
,“该中学学生既喜欢足球又喜欢游泳”为事件![]() ,然后根据积事件的概率公式
,然后根据积事件的概率公式![]()
![]() 可得结果.
可得结果.
【详解】记“该中学学生喜欢足球”为事件![]() ,“该中学学生喜欢游泳”为事件
,“该中学学生喜欢游泳”为事件![]() ,则“该中学学生喜欢足球或游泳”为事件
,则“该中学学生喜欢足球或游泳”为事件![]() ,“该中学学生既喜欢足球又喜欢游泳”为事件
,“该中学学生既喜欢足球又喜欢游泳”为事件![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
所以![]()
![]()
![]()
所以该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例为![]() .
.
故选:C.
【点睛】本题考查了积事件的概率公式,属于基础题.
本卷还有17题,登录并加入会员即可免费使用哦~

该作品由: 用户邓小军分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。