已知![]() 是无穷数列.给出两个性质:
是无穷数列.给出两个性质:
①对于![]() 中任意两项
中任意两项![]() ,在
,在![]() 中都存在一项
中都存在一项![]() ,使
,使![]() ;
;
②对于![]() 中任意项
中任意项![]() ,在
,在![]() 中都存在两项
中都存在两项![]() .使得
.使得![]() .
.
(Ⅰ)若![]() ,判断数列
,判断数列![]() 是否满足性质①,说明理由;
是否满足性质①,说明理由;
(Ⅱ)若![]() ,判断数列
,判断数列![]() 是否同时满足性质①和性质②,说明理由;
是否同时满足性质①和性质②,说明理由;
(Ⅲ)若![]() 是递增数列,且同时满足性质①和性质②,证明:
是递增数列,且同时满足性质①和性质②,证明:![]() 为等比数列.
为等比数列.
(Ⅰ)详见解析;(Ⅱ)详解解析;(Ⅲ)证明详见解析.
【解析】
【分析】
(Ⅰ)根据定义验证,即可判断;
(Ⅱ)根据定义逐一验证,即可判断;
(Ⅲ)解法一:首先,证明数列中的项数同号,然后证明![]() ,最后,用数学归纳法证明数列为等比数列即可.
,最后,用数学归纳法证明数列为等比数列即可.
解法二:首先假设数列中的项数均为正数,然后证得![]() 成等比数列,之后证得
成等比数列,之后证得![]() 成等比数列,同理即可证得数列为等比数列,从而命题得证.
成等比数列,同理即可证得数列为等比数列,从而命题得证.
【详解】(Ⅰ)![]() 不具有性质①;
不具有性质①;
(Ⅱ)![]() 具有性质①;
具有性质①;
![]() 具有性质②;
具有性质②;
(Ⅲ)【解法一】
首先,证明数列中的项数同号,不妨设恒为正数:
显然![]() ,假设数列中存在负项,设
,假设数列中存在负项,设![]() ,
,
第一种情况:若![]() ,即
,即![]() ,
,
由①可知:存在![]() ,满足
,满足![]() ,存在
,存在![]() ,满足
,满足![]() ,
,
由![]() 可知
可知![]() ,从而
,从而![]() ,与数列的单调性矛盾,假设不成立.
,与数列的单调性矛盾,假设不成立.
第二种情况:若![]() ,由①知存在实数
,由①知存在实数![]() ,满足
,满足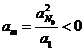 ,由
,由![]() 的定义可知:
的定义可知:![]() ,
,
另一方面,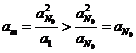 ,由数列
,由数列![]() 单调性可知:
单调性可知:![]() ,
,
这与![]() 的定义矛盾,假设不成立.
的定义矛盾,假设不成立.
同理可证得数列中的项数恒为负数.
综上可得,数列中的项数同号.
其次,证明![]() :
:
利用性质②:取![]() ,此时
,此时![]() ,
,
由数列的单调性可知![]() ,
,
而![]() ,故
,故![]() ,
,
此时必有![]() ,即
,即![]() ,
,
最后,用数学归纳法证明数列为等比数列:
假设数列![]() 的前
的前![]() 项成等比数列,不妨设
项成等比数列,不妨设![]() ,
,
其中![]() ,(
,(![]()
![]() 情况类似)
情况类似)
由①可得:存在整数![]() ,满足
,满足![]() ,且
,且![]() (*)
(*)
由②得:存在![]() ,满足:
,满足:![]() ,由数列的单调性可知:
,由数列的单调性可知:![]() ,
,
由![]() 可得:
可得:![]() (**)
(**)
由(**)和(*)式可得:![]() ,
,
结合数列的单调性有:![]() ,
,
注意到![]() 均为整数,故
均为整数,故![]() ,
,
代入(**)式,从而![]() .
.
总上可得,数列![]() 的通项公式为:
的通项公式为:![]() .
.
即数列![]() 为等比数列.
为等比数列.
【解法二】假设数列中的项数均为正数:
首先利用性质②:取![]() ,此时
,此时![]() ,
,
由数列的单调性可知![]() ,
,
而![]() ,故
,故![]() ,
,
此时必有![]() ,即
,即![]() ,
,
即![]() 成等比数列,不妨设
成等比数列,不妨设![]() ,
,
然后利用性质①:取![]() ,则
,则![]() ,
,
即数列中必然存在一项的值为![]() ,下面我们来证明
,下面我们来证明![]() ,
,
否则,由数列的单调性可知![]() ,
,
在性质②中,取![]() ,则
,则![]() ,从而
,从而![]() ,
,
与前面类似的可知则存在![]() ,满足
,满足![]() ,
,
若![]() ,则:
,则:![]() ,与假设矛盾;
,与假设矛盾;
若![]() ,则:
,则:![]() ,与假设矛盾;
,与假设矛盾;
若![]() ,则:
,则:![]() ,与数列的单调性矛盾;
,与数列的单调性矛盾;
即不存在满足题意的正整数![]() ,可见
,可见![]() 不成立,从而
不成立,从而![]() ,
,
同理可得:![]() ,从而数列
,从而数列![]() 为等比数列,
为等比数列,
同理,当数列中的项数均为负数时亦可证得数列为等比数列.
由推理过程易知数列中的项要么恒正要么恒负,不会同时出现正数和负数.
从而题中的结论得证,数列![]() 为等比数列.
为等比数列.
【点睛】本题主要考查数列的综合运用,等比数列的证明,数列性质的应用,数学归纳法与推理方法、不等式的性质的综合运用等知识,意在考查学生的转化能力和推理能力.
已知椭圆![]() 过点
过点![]() ,且
,且![]() .
.
(Ⅰ)求椭圆C的方程:
(Ⅱ)过点![]() 的直线l交椭圆C于点
的直线l交椭圆C于点![]() ,直线
,直线![]() 分别交直线
分别交直线![]() 于点
于点![]() .求
.求![]() 的值.
的值.
(Ⅰ)![]() ;(Ⅱ)1.
;(Ⅱ)1.
【解析】
【分析】
(Ⅰ)由题意得到关于a,b的方程组,求解方程组即可确定椭圆方程;
(Ⅱ)首先联立直线与椭圆的方程,然后由直线MA,NA的方程确定点P,Q的纵坐标,将线段长度的比值转化为纵坐标比值的问题,进一步结合韦达定理可证得![]() ,从而可得两线段长度的比值.
,从而可得两线段长度的比值.
【详解】(1)设椭圆方程为:![]() ,由题意可得:
,由题意可得:
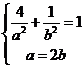 ,解得:
,解得: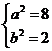 ,
,
故椭圆方程为:![]() .
.
(2)设![]() ,
,![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,
,
与椭圆方程![]() 联立可得:
联立可得:![]() ,
,
即:![]() ,
,
则:![]() .
.
直线MA的方程为:![]() ,
,
令![]() 可得:
可得:![]() ,
,
同理可得:![]() .
.
很明显![]() ,且:
,且: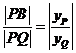 ,注意到:
,注意到:
 ,
,
而:![]()
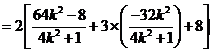
![]() ,
,
故![]() .
.
从而 .
.
【点睛】解决直线与椭圆的综合问题时,要注意:
(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;
(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.
已知函数![]() .
.
(Ⅰ)求曲线![]() 的斜率等于
的斜率等于![]() 的切线方程;
的切线方程;
(Ⅱ)设曲线![]() 在点
在点![]() 处的切线与坐标轴围成的三角形的面积为
处的切线与坐标轴围成的三角形的面积为![]() ,求
,求![]() 的最小值.
的最小值.
(Ⅰ)![]() ,(Ⅱ)
,(Ⅱ)![]() .
.
【解析】
【分析】
(Ⅰ)根据导数的几何意义可得切点的坐标,然后由点斜式可得结果;
(Ⅱ)根据导数的几何意义求出切线方程,再得到切线在坐标轴上的截距,进一步得到三角形的面积,最后利用导数可求得最值.
【详解】(Ⅰ)因为![]() ,所以
,所以![]() ,
,
设切点为![]() ,则
,则![]() ,即
,即![]() ,所以切点为
,所以切点为![]() ,
,
由点斜式可得切线方程![]() :
:![]() ,即
,即![]() .
.
(Ⅱ)显然![]() ,
,
因为![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]() ,
,
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
所以![]()
![]() ,
,
不妨设![]()
![]() 时,结果一样
时,结果一样![]() ,
,
则![]() ,
,
所以![]()
![]()
![]() ,
,
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以![]() 时,
时,![]() 取得极小值,
取得极小值,
也是最小值为![]() .
.
【点睛】本题考查了利用导数的几何意义求切线方程,考查了利用导数求函数的最值,属于中档题.
某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:
| 男生 | 女生 | |||
| 支持 | 不支持 | 支持 | 不支持 | |
| 方案一 | 200人 | 400人 | 300人 | 100人 |
| 方案二 | 350人 | 250人 | 150人 | 250人 |
假设所有学生对活动方案是否支持相互独立.
(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(Ⅱ)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(Ⅲ)将该校学生支持方案的概率估计值记为![]() ,假设该校年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为
,假设该校年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为![]() ,试比较
,试比较![]() 与
与![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)
(Ⅰ)该校男生支持方案一的概率为![]() ,该校女生支持方案一的概率为
,该校女生支持方案一的概率为![]() ;
;
(Ⅱ)![]() ,(Ⅲ)
,(Ⅲ)![]()
【解析】
【分析】
(Ⅰ)根据频率估计概率,即得结果;
(Ⅱ)先分类,再根据独立事件概率乘法公式以及分类计数加法公式求结果;
(Ⅲ)先求![]() ,再根据频率估计概率
,再根据频率估计概率![]() ,即得大小.
,即得大小.
【详解】(Ⅰ)该校男生支持方案一的概率为![]() ,
,
该校女生支持方案一的概率为![]() ;
;
(Ⅱ)3人中恰有2人支持方案一分两种情况,(1)仅有两个男生支持方案一,(2)仅有一个男生支持方案一,一个女生支持方案一,
所以3人中恰有2人支持方案一概率为:![]() ;
;
(Ⅲ)![]()
【点睛】本题考查利用频率估计概率、独立事件概率乘法公式,考查基本分析求解能力,属基础题.
在![]() 中,
中,![]() ,再从条件①、条件②这两个条件中选择一个作为己知,求:
,再从条件①、条件②这两个条件中选择一个作为己知,求:
(Ⅰ)a的值:
(Ⅱ)![]() 和
和![]() 的面积.
的面积.
条件①:![]() ;
;
条件②:![]() .
.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
选择条件①(Ⅰ)8(Ⅱ)![]() ,
, ![]() ;
;
选择条件②(Ⅰ)6(Ⅱ)![]() ,
, ![]() .
.
【解析】
【分析】
选择条件①(Ⅰ)根据余弦定理直接求解,(Ⅱ)先根据三角函数同角关系求得![]() ,再根据正弦定理求
,再根据正弦定理求![]() ,最后根据三角形面积公式求结果;
,最后根据三角形面积公式求结果;
选择条件②(Ⅰ)先根据三角函数同角关系求得![]() ,再根据正弦定理求结果,(Ⅱ)根据两角和正弦公式求
,再根据正弦定理求结果,(Ⅱ)根据两角和正弦公式求![]() ,再根据三角形面积公式求结果.
,再根据三角形面积公式求结果.
【详解】选择条件①(Ⅰ)![]()
![]()
![]()
![]()
(Ⅱ)![]()
由正弦定理得: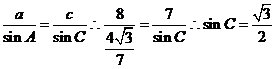
![]()
选择条件②(Ⅰ)![]()
![]()
由正弦定理得: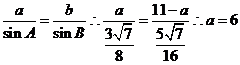
(Ⅱ)![]()
![]()
【点睛】本题考查正弦定理、余弦定理,三角形面积公式,考查基本分析求解能力,属中档题.
本卷还有16题,登录并加入会员即可免费使用哦~

该作品由: 用户cxm分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。