对于数列，若存在常数M>0，对任意的n∈N^*，恒有，则称数列为B-数列.

(1)首项为1，公比q()的等比数列是否为B-数列？请说明理由；

(2)设S_n是数列{x_n}的前n项和，给出下列两组论断：

A组：①数列{x_n}是B-数列，②数列{x_n}不是B-数列

B组：①数列{S_n}是B-数列，②数列{S_n}不是B-数列

请以其中一组的一个论断为条件，另一组的一个论断为结论组成一个命题.判断所给命题的真假，并证明你的结论.

(3)若数列{a_n}、都是B-数列，证明：数列{a_nb_n}也是B-数列

答案

（1）是B-数列（2）命题1为假命题. 命题2为真命题.（3）见解析

【详解】

解：(1)设满足条件的等比数列为{a_n}，则.于是

因此，

因为|q|<1，所以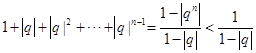

即

故首项为1，公比q(|q|<1)的等比数列是B-数列.

(2)命题1：若数列{x_n}是B-数列，则数列{S_n}也是B-数列此命题为假命题.

事实上，设x=1，n∈N^*，易知数列{x_n}是B-数列，但S_n=n，

此时.

由n的任意性，知数列{S_n}不是B-数列

命题2：若数列{S_n}是B-数列，则数列{x_n}也是B-数列此命题为真命题.

事实上，因为数列{S_n}是B-数列，所以存正数M，对任意n∈N^*有

即.于是

所以数列{x_n}是B-数列

按题中要求组成其它命题时，仿上述解法即可获得解决.

(3)若数列{a_n}、{b_n}都是B-数列，则存在正数M₁，M₂，使得对任意n∈N^*，有

，

.

注意到

同理，可得.记，则有

因此， .

故数列数列{a_nb_n}是B-数列.