已知![]() ,
,![]() ,
,![]() ,函数
,函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)当![]() 的最小值为
的最小值为![]() 时,求
时,求![]() 的值,并求
的值,并求![]() 的最小值.
的最小值.
【解析】(1)![]() ,
,
![]() 或
或![]() 或
或![]() ,
,
解得![]() 或
或![]() .·······5分
.·······5分
(2)![]() ,
,
![]()
![]() .
.
当且仅当![]() 时取得最小值
时取得最小值![]()
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 与曲线
与曲线![]() (
(![]() 为参数,
为参数,![]() ).以坐标原点为极点,
).以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)写出曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,已知点![]() 是射线
是射线![]() 与
与![]() 的公共点,点
的公共点,点![]() 是
是![]() 与
与![]() 的公共点,当
的公共点,当![]() 在区间
在区间![]() 上变化时,求
上变化时,求![]() 的最大值.
的最大值.
【解析】(1)曲线![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() .
.
曲线![]() 的普通方程为
的普通方程为![]() ,即
,即![]() ,所以曲线
,所以曲线![]() 的极坐标方程为
的极坐标方程为![]() .·······5分
.·······5分
(2)由(1)知![]() ,
,![]() ,
,
![]() ,
,
由![]() 知
知![]() ,当
,当![]() ,
,
即![]() 时,
时,![]() 有最大值
有最大值![]() .·······10分
.·······10分
已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若存在![]() ,使
,使![]() 成立,求整数
成立,求整数![]() 的最小值.
的最小值.
【解析】(1)由题意可知,![]() ,
,![]() ,·······1分
,·······1分
方程![]() 对应的
对应的![]() ,
,
当![]() ,即
,即![]() 时,当
时,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减;·······2分
上单调递减;·······2分
当![]() 时,方程
时,方程![]() 的两根为
的两根为![]() ,
,
且![]() ,
,
此时,![]() 在
在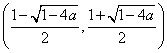 上
上![]() ,函数
,函数![]() 单调递增,
单调递增,
在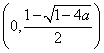 ,
,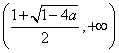 上
上![]() ,函数
,函数![]() 单调递减;·······4分
单调递减;·······4分
当![]() 时,
时,![]() ,
,![]() ,
,
此时当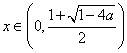 ,
,![]() ,
,![]() 单调递增,
单调递增,
当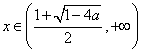 时,
时,![]() ,
,![]() 单调递减;
单调递减;
综上:当![]() 时,
时,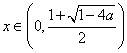 ,
,![]() 单调递增,
单调递增,
当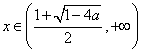 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 在
在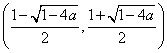 上单调递增,
上单调递增,
在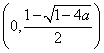 ,
,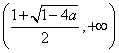 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递减;·······6分
上单调递减;·······6分
(2)原式等价于![]() ,
,
即存在![]() ,使
,使![]() 成立.
成立.
设![]() ,
,![]() ,则
,则![]() ,·······7分
,·······7分
设![]() ,
,
则![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() ,
,
根据零点存在性定理,可知![]() 在
在![]() 上有唯一零点,设该零点为
上有唯一零点,设该零点为![]() ,·······9分
,·······9分
则![]() ,且
,且![]() ,即
,即![]() ,
,
∴![]() ,
,
由题意可知![]() ,又
,又![]() ,
,![]() ,∴
,∴![]() 的最小值为5.······12分
的最小值为5.······12分
给定椭圆![]() ,称圆
,称圆![]() 为椭圆
为椭圆![]() 的“伴随圆”.已知点
的“伴随圆”.已知点![]() 是椭圆
是椭圆![]() 上的点
上的点
(1)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,求
有且只有一个公共点,求![]() 被椭圆
被椭圆![]() 的伴随圆
的伴随圆![]() 所截得的弦长:
所截得的弦长:
(2)![]() ,
,![]() 是椭圆
是椭圆![]() 上的两点,设
上的两点,设![]() ,
,![]() 是直线
是直线![]() ,
,![]() 的斜率,且满足
的斜率,且满足![]() ,试问:直线
,试问:直线![]() 是否过定点,如果过定点,求出定点坐标,如果不过定点,试说明理由.
是否过定点,如果过定点,求出定点坐标,如果不过定点,试说明理由.
【解析】(1)因为点![]() 是椭圆
是椭圆![]() 上的点.
上的点.
![]() ,
,![]() 即椭圆
即椭圆![]() ,·······2分
,·······2分
![]() ,
,![]() ,
,![]() 伴随圆
伴随圆![]() ,
,
当直线![]() 的斜率不存在时:显然不满足
的斜率不存在时:显然不满足![]() 与椭圆
与椭圆![]() 有且只有一个公共点,·······3分
有且只有一个公共点,·······3分
当直接![]() 的斜率存在时:将直线
的斜率存在时:将直线![]() 与椭圆
与椭圆![]() 联立,
联立,
得![]() ,
,
由直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点得
有且只有一个公共点得![]() ,
,
解得![]() ,由对称性取直线
,由对称性取直线![]() 即
即![]() ,
,
圆心到直线![]() 的距离为
的距离为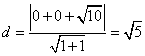 ,
,
直线![]() 被椭圆
被椭圆![]() 的伴随圆
的伴随圆![]() 所截得的弦长
所截得的弦长![]() ,·······6分
,·······6分
(2)设直线![]() ,
,![]() 的方程分别为
的方程分别为![]() ,
,![]() ,
,
设点![]() ,
,![]() ,
,
联立![]() 得
得![]() ,
,
则![]() 得
得![]() 同理
同理![]() ,·······8分
,·······8分
斜率![]() ,·······9分
,·······9分
同理![]() ,因为
,因为![]() ,·······10分
,·······10分
所以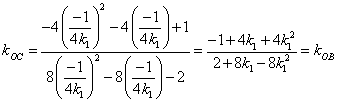 ,
,
![]() ,
,![]() ,
,![]() 三点共线,即直线
三点共线,即直线![]() 过定点
过定点![]() .·······12分
.·······12分
如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
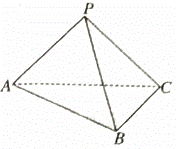
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若动点![]() 在底面
在底面![]() 边界及内部,二面角
边界及内部,二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的最小值.
的最小值.
【解析】(1)取![]() 中点
中点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() .
.
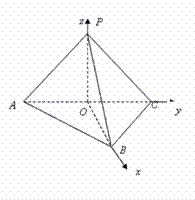
以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立如图所示空间直角坐标系,
轴建立如图所示空间直角坐标系,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,·······2分
,·······2分
设平面![]() 的法向量
的法向量![]() ,由
,由![]() ,
,![]() 得方程组
得方程组![]() ,取
,取![]() ,·······4分
,·······4分
∴![]() .·······5分
.·······5分
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .·······6分
.·······6分
(2)由题意平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴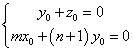 ,取
,取![]() ,·······9分
,·······9分
∴![]() .∴
.∴![]() ,∴
,∴![]() 或
或![]() (舍去).
(舍去).
∴![]() 点到
点到![]() 的最小值为垂直距离
的最小值为垂直距离![]() .·······12分
.·······12分
本卷还有18题,登录并加入会员即可免费使用哦~

该作品由: 用户123分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。