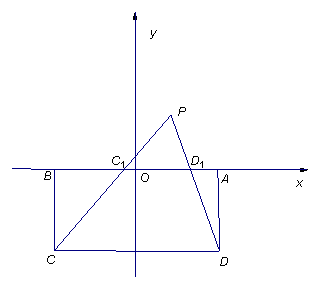
数学家斐波那契在其所著《计算之书》中，记有“二鸟饮泉”间题，题意如下：“如图1，两塔相距步，高分别为步和步.两塔间有喷泉，塔顶各有一鸟.两鸟同时自塔顶出发，沿直线飞往喷泉，同时抵达（假设两鸟速度相同）.求两塔与喷泉中心之距.”如图2，现有两塔、，底部、相距12米，塔高3米，塔高9米.假设塔与地面垂直，小鸟飞行路线与两塔在同一竖直平面内.

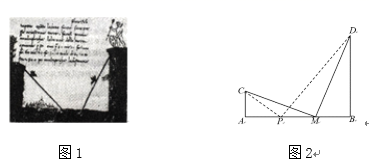
（1）若如《计算之书》所述，有飞行速度相同的两鸟，同时从塔顶出发，同时抵达喷泉所在点，求喷泉距塔底的距离；

（2）若塔底、之间为喷泉形成的宽阔的水面，一只小鸟从塔顶出发，飞抵水面、 之间的某点处饮水之后，飞到对面的塔顶处.求当小鸟飞行距离最短时，饮水点到塔底的距离.

答案

（1）9米；（2）3米.

【分析】

（1）设，列方程求解；

（2）作出关于的对称点，与的交点就是最短距离的点，由此可计算出结论．

【详解】

（1）设，则由题意，解得；

（2）设是关于直线的对称点，连接交于，

是线段上任一点，如图，，当且仅当与重合时，等号成立．点即为所求．

∵，∴，∴，而，∴，解得．

【点睛】

本题考查数学文化，考查数学的应用，解题关键是正确理解题意，抽象出数学问题，用相应的数学知识求解．