已知 a , b , c 均为正数,且 ,证明:
(1) ;
(2) 若 ,则
.
(1) 见解析
(2) 见解析
【分析】( 1 )方法一:根据 ,利用柯西不等式即可得证;
( 2 )由( 1 )结合已知可得 ,即可得到
,再根据权方和不等式即可得证 .
【详解】( 1 ) [ 方法一 ] :【最优解】柯西不等式
由柯西不等式有 ,
所以 ,当且仅当
时,取等号,所以
.
[ 方法二 ] :基本不等式
由 ,
,
,
,
当且仅当 时,取等号,所以
.
( 2 )证明:因为 ,
,
,
,由( 1 )得
,
即 ,所以
,
由权方和不等式知 ,
当且仅当 ,即
,
时取等号,
所以 .
【点睛】( 1 )方法一:利用柯西不等式证明,简洁高效,是该题的最优解;
方法二:对于柯西不等式不作为必须掌握内容的地区同学,采用基本不等式累加,也是不错的方法.
设集合 ,则
( )
A . B .
C .
D .
A
【分析】根据集合的交集运算即可解出.
【详解】因为 ,
,所以
.
故选: A.
某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取 10 位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这 10 位社区居民在讲座前和讲座后问卷答题的正确率如下图:
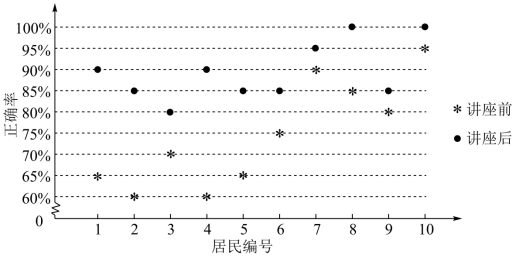
则( )
A .讲座前问卷答题的正确率的中位数小于
B .讲座后问卷答题的正确率的平均数大于
C .讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D .讲座后问卷答题的正确率的极差大于讲座前正确率的极差
B
【分析】由图表信息,结合中位数、平均数、标准差、极差的概念,逐项判断即可得解 .
【详解】讲座前中位数为 , 所以
错;
讲座后问卷答题的正确率只有一个是 个
, 剩下全部大于等于
, 所以讲座后问卷答题的正确率的平均数大于
, 所以 B 对;
讲座前问卷答题的正确率更加分散 , 所以讲座前问卷答题的正确率的标准差大于讲座后正确率的标准差 , 所以 C 错;
讲座后问卷答题的正确率的极差为 ,
讲座前问卷答题的正确率的极差为 , 所以
错 .
故选 :B.
若 .则
( )
A . B .
C .
D .
D
【分析】根据复数代数形式的运算法则,共轭复数的概念以及复数模的计算公式即可求出.
【详解】因为 ,所以
,所以
.
故选: D.
如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为 1 ,则该多面体的体积为( )
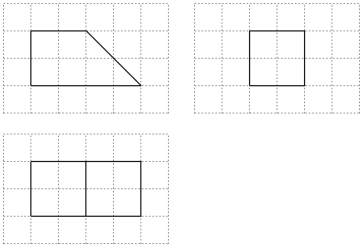
A . 8 B . 12 C . 16 D . 20
B
【分析】由三视图还原几何体,再由棱柱的体积公式即可得解 .
【详解】由三视图还原几何体,如图,
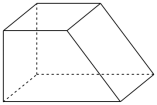
则该直四棱柱的体积 .
故选: B.
将函数 的图像向左平移
个单位长度后得到曲线 C ,若 C 关于 y 轴对称,则
的最小值是( )
A . B .
C .
D .
C
【分析】先由平移求出曲线 的解析式,再结合对称性得
,即可求出
的最小值 .
【详解】由题意知:曲线 为
,又
关于
轴对称,则
,
解得 ,又
,故当
时,
的最小值为
.
故选: C.
从分别写有 1 , 2 , 3 , 4 , 5 , 6 的 6 张卡片中无放回随机抽取 2 张,则抽到的 2 张卡片上的数字之积是 4 的倍数的概率为( )
A . B .
C .
D .
C
【分析】方法一:先列举出所有情况,再从中挑出数字之积是 4 的倍数的情况,由古典概型求概率即可 .
【详解】 [ 方法一 ] :【最优解】无序
从 6 张卡片中无放回抽取 2 张,共有 15 种情况,其中数字之积为 4 的倍数的有
6 种情况,故概率为
.
[ 方法二 ] :有序
从 6 张卡片中无放回抽取 2 张,共有 ,(2,1),(3,1),(4,1),(5,1),(6,1),(3,2),(4,2),(5,2),(6,2),(4,3),(5,3),(6,3),(5,4),(6,4),(6,5)30 种情况,
其中数字之积为 4 的倍数有 (1,4),(2,4),(2,6),(3,4),(4,1),(4,2),(4,3),(4,5),(4,6),(5,4),(6,2),(6,4)12 种情况,故概率为 .
故选: C.
【整体点评】方法一:将抽出的卡片看成一个组合,再利用古典概型的概率公式解出,是该题的最优解;
方法二:将抽出的卡片看成一个排列,再利用古典概型的概率公式解出;
函数 在区间
的图象大致为( )
A . 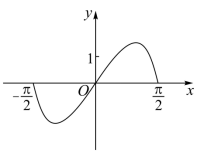 B .
B . 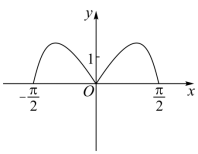
C .  D .
D . 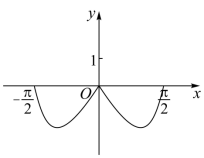
A
【分析】由函数的奇偶性结合指数函数、三角函数的性质逐项排除即可得解 .
【详解】令 ,
则 ,
所以 为奇函数,排除 BD ;
又当 时,
,所以
,排除 C.
故选: A.
当 时,函数
取得最大值
,则
( )
A . B .
C .
D . 1
B
【分析】根据题意可知 ,
即可解得
,再根据
即可解出.
【详解】因为函数 定义域为
,所以依题可知,
,
,而
,所以
,即
,所以
,因此函数
在
上递增,在
上递减,
时取最大值,满足题意,即有
.
故选: B.
在长方体 中,已知
与平面
和平面
所成的角均为
,则( )
A . B . AB 与平面
所成的角为
C . D .
与平面
所成的角为
D
【分析】根据线面角的定义以及长方体的结构特征即可求出.
【详解】如图所示:

不妨设 ,依题以及长方体的结构特征可知,
与平面
所成角为
,
与平面
所成角为
,所以
,即
,
,解得
.
对于 A , ,
,
, A 错误;
对于 B ,过 作
于
,易知
平面
,所以
与平面
所成角为
,因为
,所以
, B 错误;
对于 C , ,
,
, C 错误;
对于 D , 与平面
所成角为
,
,而
,所以
. D 正确.
故选: D .
甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为 ,侧面积分别为
和
,体积分别为
和
.若
,则
( )
A . B .
C .
D .
C
【分析】设母线长为 ,甲圆锥底面半径为
,乙圆锥底面圆半径为
,根据圆锥的侧面积公式可得
,再结合圆心角之和可将
分别用
表示,再利用勾股定理分别求出两圆锥的高,再根据圆锥的体积公式即可得解 .
【详解】解:设母线长为 ,甲圆锥底面半径为
,乙圆锥底面圆半径为
,
则 ,
所以 ,
又 ,
则 ,
所以 ,
所以甲圆锥的高 ,
乙圆锥的高 ,
所以 .
故选: C.
已知椭圆 的离心率为
,
分别为 C 的左、右顶点, B 为 C 的上顶点.若
,则 C 的方程为( )
A . B .
C .
D .
B
【分析】根据离心率及 ,解得关于
的等量关系式,即可得解 .
【详解】解:因为离心率 ,解得
,
,
分别为 C 的左右顶点,则
,
B 为上顶点,所以 .
所以 ,因为
所以 ,将
代入,解得
,
故椭圆的方程为 .
故选: B.
已知向量 .若
,则
.
/
【分析】直接由向量垂直的坐标表示求解即可 .
【详解】由题意知: ,解得
.
故答案为: .
已知 ,则( )
A . B .
C .
D .
A
【分析】法一:根据指对互化以及对数函数的单调性即可知 ,再利用基本不等式,换底公式可得
,
,然后由指数函数的单调性即可解出.
【详解】 [方法一]:(指对数函数性质)
由 可得
,而
,所以
,即
,所以
.
又 ,所以
,即
,
所以 . 综上,
.
[方法二]:【最优解】(构造函数)
由 ,可得
.
根据 的形式构造函数
,则
,
令 ,解得
,由
知
.
在
上单调递增,所以
,即
,
又因为 ,所以
.
故选: A.
【点评】法一:通过基本不等式和换底公式以及对数函数的单调性比较,方法直接常用,属于通性通法;
法二:利用 的形式构造函数
,根据函数的单调性得出大小关系,简单明了,是该题的最优解.
在直角坐标系 中,曲线
的参数方程为
( t 为参数),曲线
的参数方程为
( s 为参数).
(1) 写出 的普通方程;
(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
,求
与
交点的直角坐标,及
与
交点的直角坐标.
(1) ;
(2) 的交点坐标为
,
,
的交点坐标为
,
.
【分析】 (1) 消去 ,即可得到
的普通方程;
(2) 将曲线 的方程化成普通方程,联立求解即解出.
【详解】( 1 )因为 ,
,所以
,即
的普通方程为
.
( 2 )因为 ,所以
,即
的普通方程为
,
由 ,即
的普通方程为
.
联立 ,解得:
或
,即交点坐标为
,
;
联立 ,解得:
或
,即交点坐标为
,
.
设抛物线 的焦点为 F ,点
,过 F 的直线交 C 于 M , N 两点.当直线 MD 垂直于 x 轴时,
.
(1) 求 C 的方程;
(2) 设直线 与 C 的另一个交点分别为 A , B ,记直线
的倾斜角分别为
.当
取得最大值时,求直线 AB 的方程.
(1) ;
(2) .
【分析】( 1 )由抛物线的定义可得 ,即可得解;
( 2 )法一:设点的坐标及直线 ,由韦达定理及斜率公式可得
,再由差角的正切公式及基本不等式可得
,设直线
,结合韦达定理可解 .
【详解】( 1 )抛物线的准线为 ,当
与 x 轴垂直时,点 M 的横坐标为 p ,
此时 ,所以
,
所以抛物线 C 的方程为 ;
( 2 ) [ 方法一 ] :【最优解】直线方程横截式
设 ,直线
,
由 可得
,
,
由斜率公式可得 ,
,
直线 ,代入抛物线方程可得
,
,所以
,同理可得
,
所以
又因为直线 MN 、 AB 的倾斜角分别为 ,所以
,
若要使 最大,则
,设
,则
,
当且仅当 即
时,等号成立,
所以当 最大时,
,设直线
,
代入抛物线方程可得 ,
,所以
,
所以直线 .
[ 方法二 ] :直线方程点斜式
由题可知,直线 MN 的斜率存在 .
设 , 直线
由 得:
,
, 同理,
.
直线 MD : , 代入抛物线方程可得:
,同理,
.
代入抛物线方程可得 : , 所以
,同理可得
,
由斜率公式可得:
(下同方法一)若要使 最大,则
,
设 ,则
,
当且仅当 即
时,等号成立,
所以当 最大时,
,设直线
,
代入抛物线方程可得 ,
,所以
,所以直线
.
[ 方法三 ] :三点共线
设 ,
设 , 若 P 、 M 、 N 三点共线,由
所以 ,化简得
,
反之,若 , 可得 MN 过定点
因此,由 M 、 N 、 F 三点共线,得 ,
由 M 、 D 、 A 三点共线,得 ,
由 N 、 D 、 B 三点共线,得 ,
则 , AB 过定点( 4,0 )
(下同方法一)若要使 最大,则
,
设 ,则
,
当且仅当 即
时,等号成立,
所以当 最大时,
,所以直线
.
【整体点评】( 2 )法一:利用直线方程横截式,简化了联立方程的运算,通过寻找直线 的斜率关系,由基本不等式即可求出直线 AB 的斜率,再根据韦达定理求出直线方程,是该题的最优解,也是通性通法;
法二:常规设直线方程点斜式,解题过程同解法一;
法三:通过设点由三点共线寻找纵坐标关系,快速找到直线 过定点,省去联立过程,也不失为一种简化运算的好方法.
已知函数 ,曲线
在点
处的切线也是曲线
的切线.
(1) 若 ,求 a ;
(2) 求 a 的取值范围.
(1)3
(2)
【分析】( 1 )先由 上的切点求出切线方程,设出
上的切点坐标,由斜率求出切点坐标,再由函数值求出
即可;
( 2 )设出 上的切点坐标,分别由
和
及切点表示出切线方程,由切线重合表示出
,构造函数,求导求出函数值域,即可求得
的取值范围 .
【详解】( 1 )由题意知, ,
,
,则
在点
处的切线方程为
,
即 ,设该切线与
切于点
,
,则
,解得
,则
,解得
;
( 2 ) ,则
在点
处的切线方程为
,整理得
,
设该切线与 切于点
,
,则
,则切线方程为
,整理得
,
则 ,整理得
,
令 ,则
,令
,解得
或
,
令 ,解得
或
,则
变化时,
的变化情况如下表:
| | | | | 0 | | 1 | |
| | | 0 | | 0 | | 0 | |
| | | | | | | | |
则 的值域为
,故
的取值范围为
.
小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面 是边长为 8 (单位:
)的正方形,
均为正三角形,且它们所在的平面都与平面
垂直.
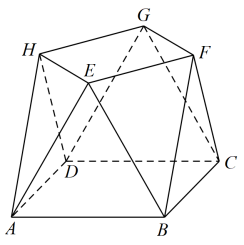
(1) 证明: 平面
;
(2) 求该包装盒的容积(不计包装盒材料的厚度).
(1) 证明见解析;
(2) .
【分析】( 1 )分别取 的中点
,连接
,由平面知识可知
,
,依题从而可证
平面
,
平面
,根据线面垂直的性质定理可知
,即可知四边形
为平行四边形,于是
,最后根据线面平行的判定定理即可证出;
( 2 )再分别取 中点
,由( 1 )知,该几何体的体积等于长方体
的体积加上四棱锥
体积的
倍,即可解出.
【详解】( 1 )如图所示:
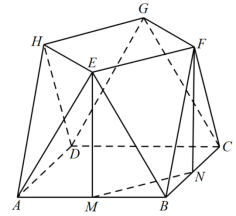
分别取 的中点
,连接
,因为
为全等的正三角形,所以
,
,又平面
平面
,平面
平面
,
平面
,所以
平面
,同理可得
平面
,根据线面垂直的性质定理可知
,而
,所以四边形
为平行四边形,所以
,又
平面
,
平面
,所以
平面
.
( 2 ) [ 方法一 ] :分割法一
如图所示:
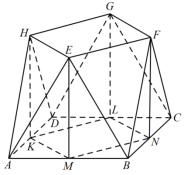
分别取 中点
,由( 1 )知,
且
,同理有,
,
,
,由平面知识可知,
,
,
,所以该几何体的体积等于长方体
的体积加上四棱锥
体积的
倍.
因为 ,
,点
到平面
的距离即为点
到直线
的距离
,
,所以该几何体的体积
.
[ 方法二 ] :分割法二
如图所示:
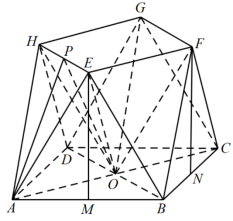
连接 AC,BD, 交于 O ,连接 OE,OF,OG,OH. 则该几何体的体积等于四棱锥 O-EFGH 的体积加上三棱锥 A-OEH 的 倍 , 再加上三棱锥 E-OAB 的四倍.容易求得, OE=OF=OG=OH=8, 取 EH 的中点 P ,连接 AP,OP. 则 EH 垂直平面 APO. 由图可知,三角形 APO, 四棱锥 O-EFGH 与三棱锥 E-OAB 的高均为 EM 的长 . 所以该几何体的体积
甲、乙两城之间的长途客车均由 A 和 B 两家公司运营,为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的 500 个班次,得到下面列联表:
| | 准点班次数 | 未准点班次数 |
| A | 240 | 20 |
| B | 210 | 30 |
(1) 根据上表,分别估计这两家公司甲、乙两城之间的长途客车准点的概率;
(2) 能否有 90% 的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关?
附: ,
| | 0.100 | 0.050 | 0.010 |
| | 2.706 | 3.841 | 6.635 |
(1) A , B 两家公司长途客车准点的概率分别为 ,
(2) 有
【分析】( 1 )根据表格中数据以及古典概型的概率公式可求得结果;
( 2 )根据表格中数据及公式计算 ,再利用临界值表比较即可得结论 .
【详解】( 1 )根据表中数据, A 共有班次 260 次,准点班次有 240 次,
设 A 家公司长途客车准点事件为 M ,
则 ;
B 共有班次 240 次,准点班次有 210 次,
设 B 家公司长途客车准点事件为 N ,
则 .
A 家公司长途客车准点的概率为 ;
B 家公司长途客车准点的概率为 .
( 2 )列联表
| | 准点班次数 | 未准点班次数 | 合计 |
| A | 240 | 20 | 260 |
| B | 210 | 30 | 240 |
| 合计 | 450 | 50 | 500 |
=
,
根据临界值表可知,有 的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关 .
记 为数列
的前 n 项和.已知
.
(1) 证明: 是等差数列;
(2) 若 成等比数列,求
的最小值.
(1) 证明见解析;
(2) .
【分析】( 1 )依题意可得 ,根据
,作差即可得到
,从而得证;
( 2 )法一:由( 1 )及等比中项的性质求出 ,即可得到
的通项公式与前
项和,再根据二次函数的性质计算可得.
【详解】( 1 )因为 ,即
① ,
当 时,
② ,
① ② 得,
,
即 ,
即 ,所以
,
且
,
所以 是以
为公差的等差数列.
( 2 ) [ 方法一 ] :二次函数的性质
由( 1 )可得 ,
,
,
又 ,
,
成等比数列,所以
,
即 ,解得
,
所以 ,所以
,
所以,当 或
时,
.
[ 方法二 ] :【最优解】邻项变号法
由( 1 )可得 ,
,
,
又 ,
,
成等比数列,所以
,
即 ,解得
,
所以 ,即有
.
则当 或
时,
.
【整体点评】( 2 )法一:根据二次函数的性质求出 的最小值,适用于可以求出
的表达式;
法二:根据邻项变号法求最值,计算量小,是该题的最优解.
查看答案
单次付费有效 3.99 元
用于查看答案,单次有效 19.99元
包月VIP 9.99 元
用于查看答案,包月VIP无限次 49.99元